A circular conducting ring is rotated about one its diameter in a magnetic field
If magnetic field is uniform, no emf will be induced
If magnetic field is uniform and its induction increases with time, only them emf is induced
If magnetic field is uniform and induction of magnetic field is increasing at a constant rate, emf induced in ring may zero for an elemental time interval
None of these
The correct Answer is:D
To solve the problem of a circular conducting ring being rotated about one of its diameters in a magnetic field, we need to analyze how the magnetic flux through the ring changes as it rotates. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a circular conducting ring that is rotated about one of its diameters in a magnetic field. The magnetic field can be uniform or non-uniform.
Hint: Visualize the ring and the magnetic field lines to understand their orientation relative to the ring.
Step 2: Determine the Magnetic Flux
Magnetic flux (Φ) through the ring is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the ring,
- θ is the angle between the magnetic field and the normal to the surface of the ring.
Hint: Remember that the area of the ring remains constant, but the angle θ changes as the ring rotates.
Step 3: Analyze the Rotation
As the ring rotates about its diameter, the angle θ changes continuously. When the plane of the ring is perpendicular to the magnetic field, θ=0° and the flux is maximum. When the plane of the ring is parallel to the magnetic field, θ=90° and the flux is zero.
Hint: Think about how the orientation of the ring affects the angle θ and thus the magnetic flux.
Step 4: Induced EMF Calculation
According to Faraday's law of electromagnetic induction, the induced EMF (ε) in the ring is given by the rate of change of magnetic flux:
ε=−dΦdt
As the ring rotates, Φ changes with time, leading to a non-zero induced EMF.
Hint: Consider how the change in angle affects the rate of change of flux over time.
Step 5: Conclusion
If the magnetic field is uniform and the ring is rotating, there will be an induced EMF due to the changing magnetic flux. If the magnetic field is non-uniform, the situation becomes more complex, but the principle remains the same: a change in flux leads to induced EMF.
Hint: Reflect on the conditions under which EMF is induced and how they relate to the uniformity of the magnetic field.
Final Answer
In conclusion, as the circular conducting ring rotates in a magnetic field, an EMF will be induced due to the changing magnetic flux through the ring.
---
We have a circular conducting ring that is rotated about one of its diameters in a magnetic field. The magnetic field can be uniform or non-uniform.
Magnetic flux (Φ) through the ring is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the ring,
- θ is the angle between the magnetic field and the normal to the surface of the ring.
As the ring rotates about its diameter, the angle θ changes continuously. When the plane of the ring is perpendicular to the magnetic field, θ=0° and the flux is maximum. When the plane of the ring is parallel to the magnetic field, θ=90° and the flux is zero.
According to Faraday's law of electromagnetic induction, the induced EMF (ε) in the ring is given by the rate of change of magnetic flux:
ε=−dΦdt
As the ring rotates, Φ changes with time, leading to a non-zero induced EMF.
If the magnetic field is uniform and the ring is rotating, there will be an induced EMF due to the changing magnetic flux. If the magnetic field is non-uniform, the situation becomes more complex, but the principle remains the same: a change in flux leads to induced EMF.
In conclusion, as the circular conducting ring rotates in a magnetic field, an EMF will be induced due to the changing magnetic flux through the ring.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
46 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION -J(Aakash Challengers Questions)
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA unifrom circular disc of mass 200g and radius 4cm is rotated about one of its diameters at an angular speed of 10rad/s. Find its abgular momentum about the axis of rotation ?
View Solution
Knowledge Check
A coil of 500 turns and mean radius 10 cm makes 3000 rotations per minute about one of its diameter in a uniform magnetic field of induction 4×10−2Wb/m2 perpendicular to its axis of rotation. The rms current through the coil if its resistance is 100 Ω, is
A4.1AB1.4AC4.4AD1.1AIf a conductor is rotating about its one end in a uniform magnetic field then an emf induced in it is
Ae=−BAfBe=+BAf2Ce=B/AfDe=BA charge q is spread uniformly over an isolated ring of radius 'R'. The ring is rotated about its natural axis and has magnetic dipole moment of the ring as M. Angular velocity of rotation is
AM2qR2BM(qR)2C2MqR2DqM2R
Statement 1: The net force on a closed circular current carrying loop placed in a uniform magnetic field is zero.
Statement 2: The torque produced in a conducting circular ring is zero when it is placed in a uniform magnetic field such that the magnetic field is perpendicular to the plane of loop.
View SolutionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
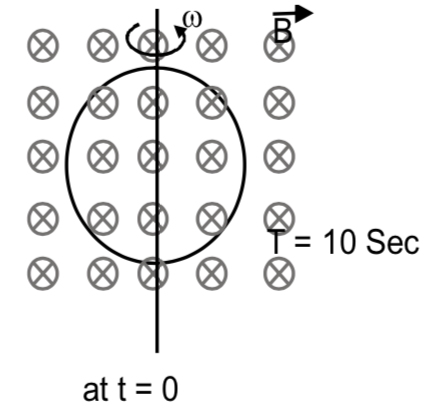 )
)
View SolutionAB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R1 and R2 do not rotate. Then the current through the resistor R1 is
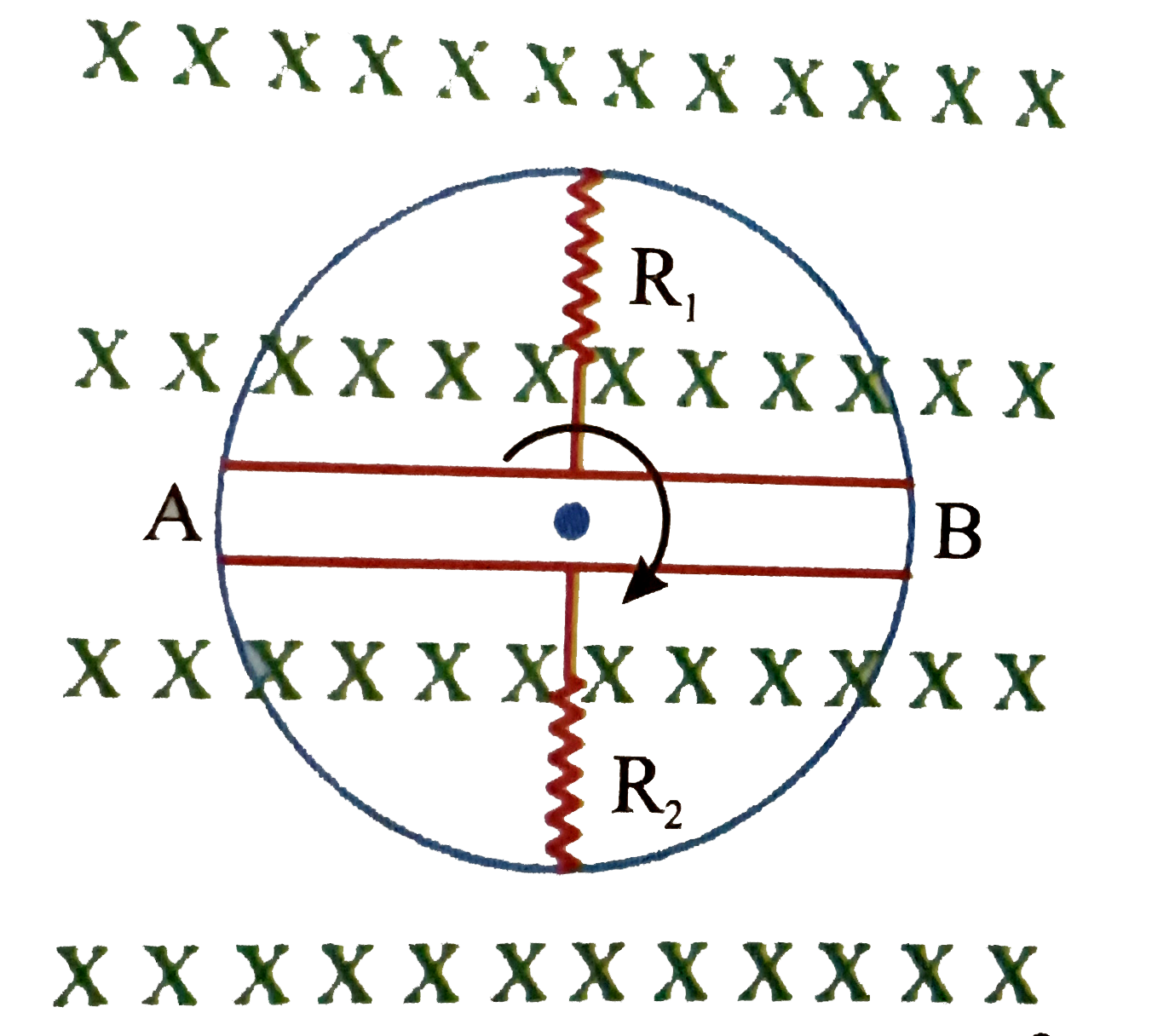
View SolutionA conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View Solution
