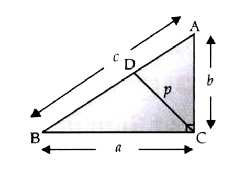
ABC is right angle triangle at C. Let BC = a, CA = b, AB = c and Let 'P' be the length of perpendicular from C to AB. prove that $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$

Video Solution

Text Solution

Verified by Experts

Area of triangle $A B C, (A) = \frac{1}{2} * b a s e * h e i g h t = \frac{1}{2} \cdot a * b = \frac{a b}{2}$
As length of prependicular is $p$ from $A B$ ,
$∴$ Area $(A) = \frac{1}{2} * c * p = \frac{c p}{2}$
$∴ \frac{a b}{2} = \frac{c p}{2} \Rightarrow a b = c p$
$c = \frac{a b}{p} \to (1)$
As $Δ A B C$ is a right angle triangle,
$∴ a^{2} + b^{2} = c^{2}$
From (1),
$a^{2} + b^{2} = {(\frac{a b}{p})}^{2}$
$\Rightarrow \frac{a^{2} + b^{2}}{a^{2} b^{2}} = \frac{1}{p^{2}}$
$\Rightarrow \frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$

ABC is a right angled triangle in which $∠ C = 90^{\circ}$ . If $B C = a, A B = c, C A = b$ and the length of perpendicular from C to AB be p. then, $\frac{1}{a^{2}} + \frac{1}{b^{2}} = ?$
A $\frac{1}{p}$
B $\frac{2}{p^{2}}$
C $\frac{1}{p^{2}}$
DNone of these
In a $Δ A B C$ right angle at C .P is the length of $⊥$ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A $\frac{1}{p^{2}} = \frac{1}{b^{2}} - \frac{1}{a^{2}}$
B $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
C $\frac{1}{p^{2}} + \frac{1}{a^{2}} = - \frac{1}{b^{2}}$
D $\frac{1}{p^{2}} = \frac{1}{a^{2}} - \frac{1}{b^{2}}$