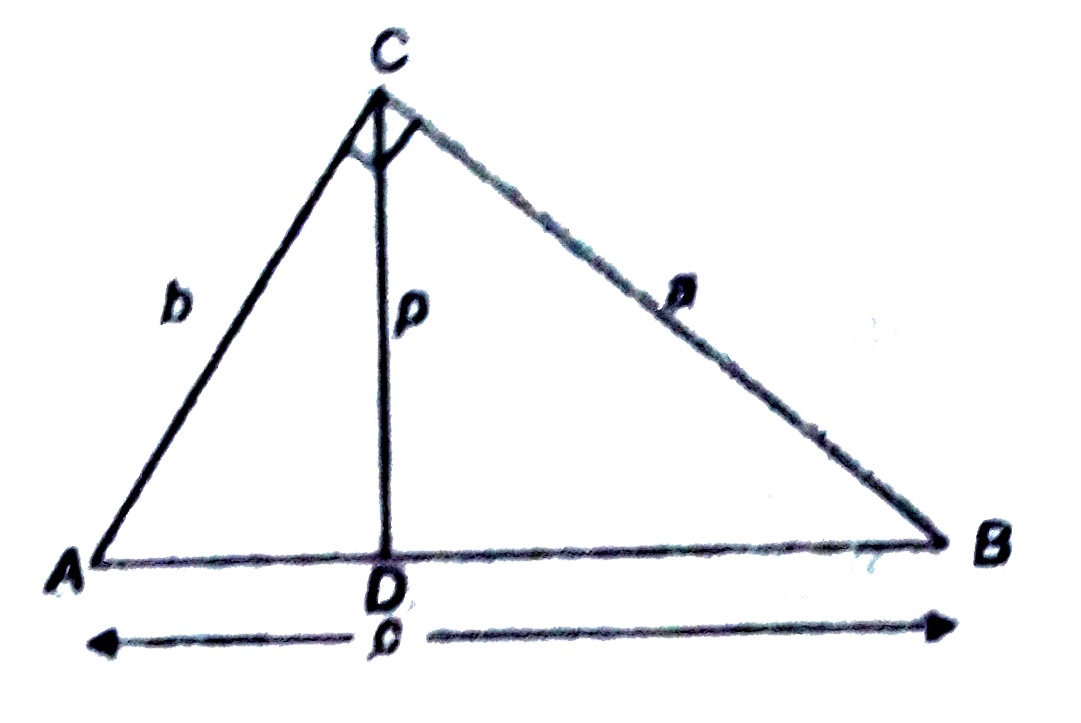
ABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$

Video Solution

Text Solution

Verified by Experts

ABC is a right angled , at C, p is the lenth of the perpendicular from C to AB.
Proof: (i) $a r (△ A B C) = \frac{1}{2} \times A B \times C D$
$\frac{1}{2} c p$
$A l s o a r (△ A B C) = \frac{1}{2} \times A C \times B C$
= $\frac{1}{2} b a \dots . . (2)$
from (1) and (2) , we get
$\frac{1}{2} p c = \frac{1}{2} a b$
pc=ab ....(3)
(i) from (3) we get $c = \frac{a b}{p}$
$I n △ A B C$
$c^{2} = a^{2} + b^{2}$ ( by Pythagoras theorem)
${(\frac{a b}{P})}^{2} = a^{2} + b^{2} \Rightarrow \frac{a^{2} b^{2}}{P^{2}} = a^{2} + b^{2}$
$\frac{1}{P^{2}} = \frac{a^{2} + b^{2}}{a^{2} b^{2}} \Rightarrow \frac{1}{P^{2}} = \frac{a^{2}}{a^{2} b^{2}} + \frac{b^{2}}{a^{2} b^{2}}$
$\frac{1}{P^{2}} = \frac{1}{b^{2}} + \frac{1}{a^{2}}$
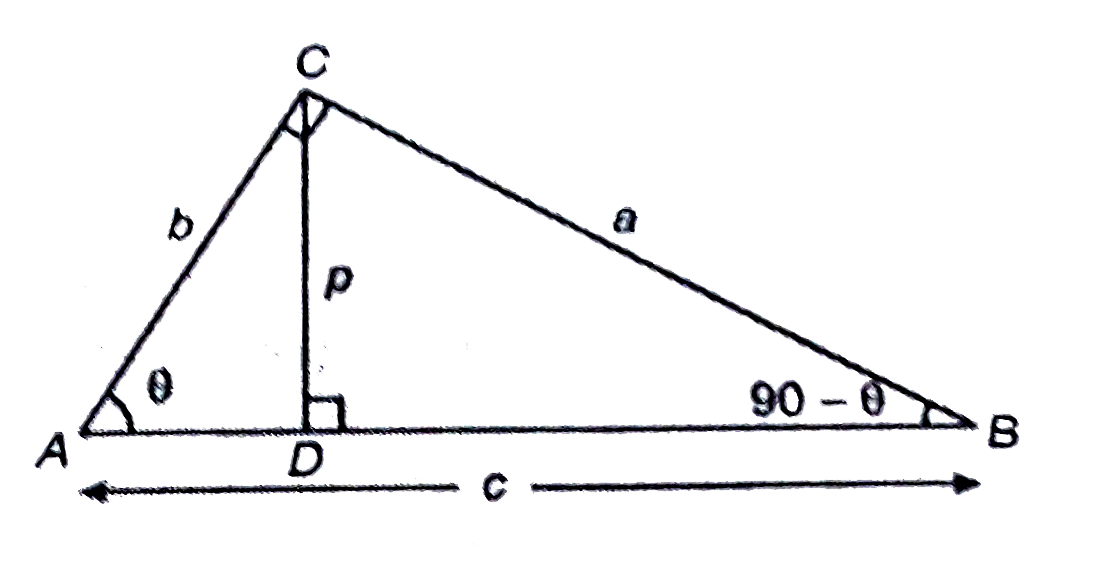
Alternative proof ( using trigonometry) let $∠ C A B = θ$
$∠ C B A = 90^{\circ} - θ (∠ A C B = 90^{\circ})$
In right $△ C D A$
$sin θ = \frac{p}{b}$
in right $△ C D B$
$sin (90 - θ) = \frac{p}{a}$
$\Rightarrow cos θ = \frac{p}{a}$
squaring and adding equations (1) and (2) , we get
$sin θ + {cos}^{2} θ = \frac{p^{2}}{b^{2}} + \frac{p^{2}}{a^{2}}$
$1 = p^{2} ((\frac{1}{a^{2}} + \frac{1}{b^{2}}) (u sin g n t i t y {sin}^{2} θ + {cos}^{2} θ = 1)$
$\Rightarrow \frac{1}{P^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
Remark : you will read $sin (90 - θ) cos θ and {sin}^{2} θ + {cos}^{2} θ = 1$ in the later chapter 8.

In a $Δ A B C$ right angle at C .P is the length of $⊥$ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A $\frac{1}{p^{2}} = \frac{1}{b^{2}} - \frac{1}{a^{2}}$
B $\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
C $\frac{1}{p^{2}} + \frac{1}{a^{2}} = - \frac{1}{b^{2}}$
D $\frac{1}{p^{2}} = \frac{1}{a^{2}} - \frac{1}{b^{2}}$
ABC is a right angled triangle in which $∠ C = 90^{\circ}$ . If $B C = a, A B = c, C A = b$ and the length of perpendicular from C to AB be p. then, $\frac{1}{a^{2}} + \frac{1}{b^{2}} = ?$
A $\frac{1}{p}$
B $\frac{2}{p^{2}}$
C $\frac{1}{p^{2}}$
DNone of these