In the figure, E is any point on median AD of a △ABC. Show that ar(△ABE)= ar(△ACE).
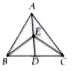
Step by step video, text & image solution for In the figure, E is any point on median AD of a triangleABC. Show that ar(triangleABE)= ar(triangleACE). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Multiple Choice Questions )
45 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.2)
7 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
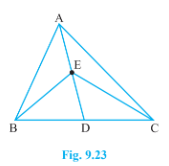
View SolutionIn the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionE is any point on median AD of AABC If ar(△ABE) = 10 cm thenar(△ACE) is
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).

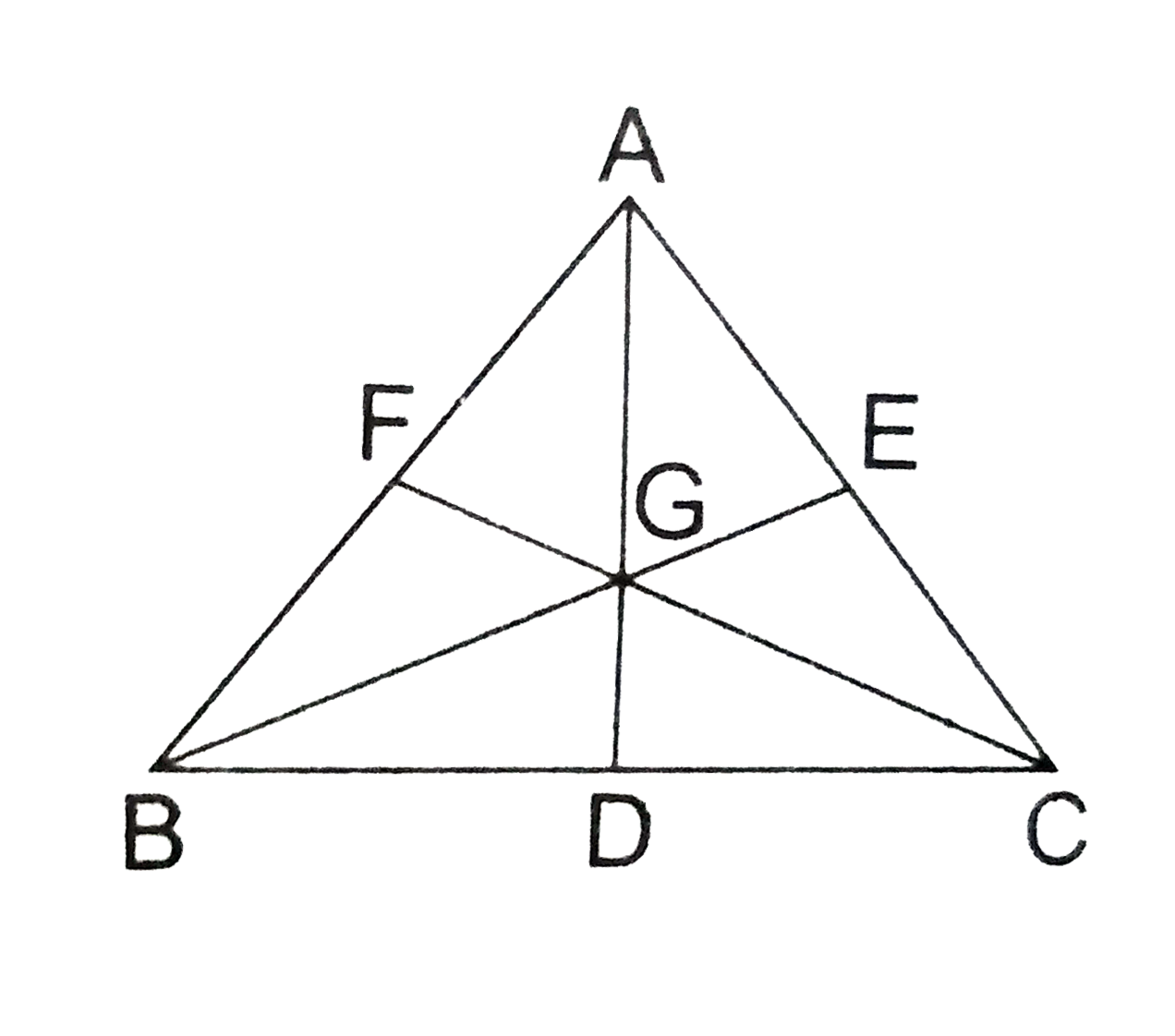
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
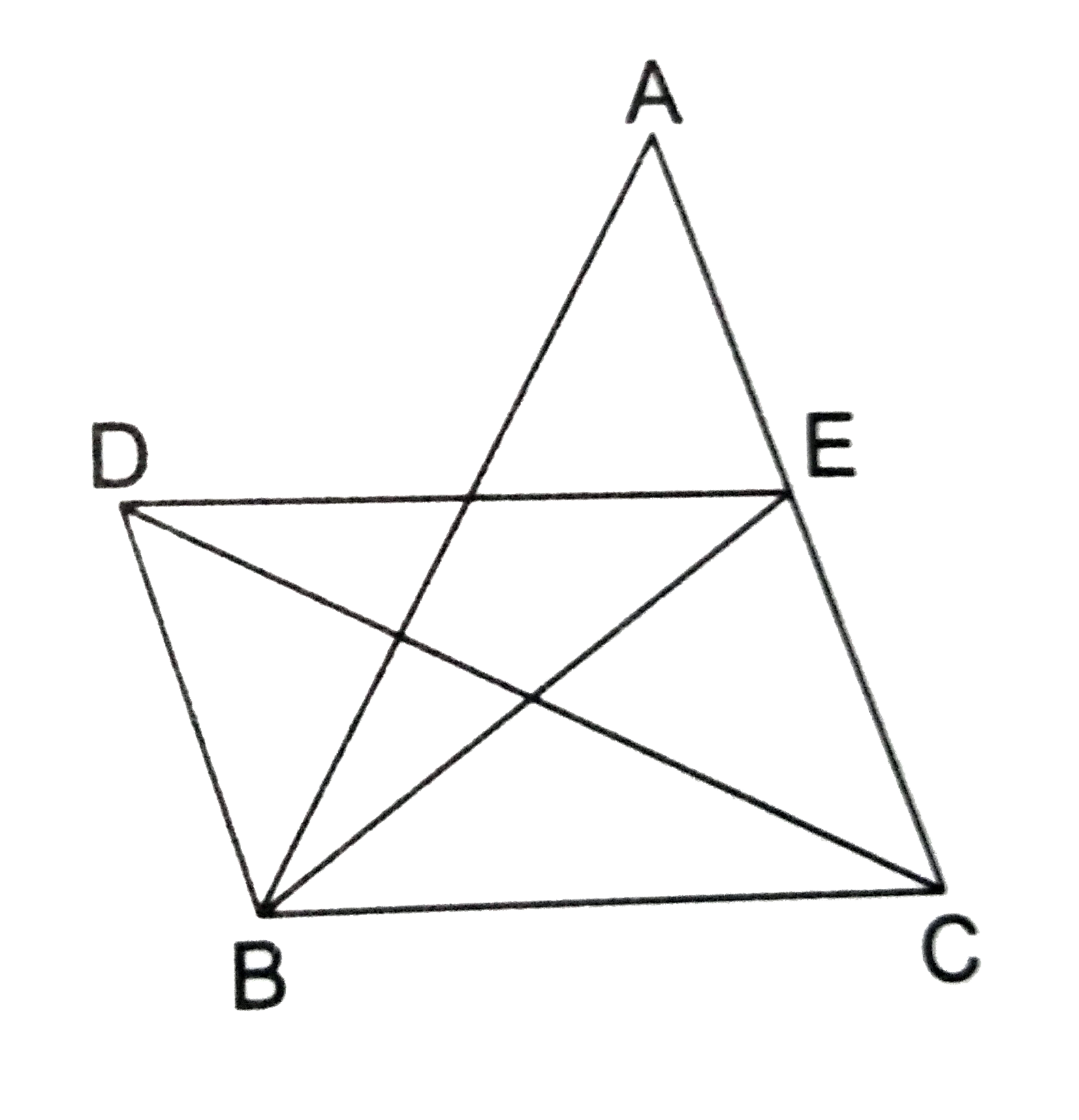
View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
View Solution
