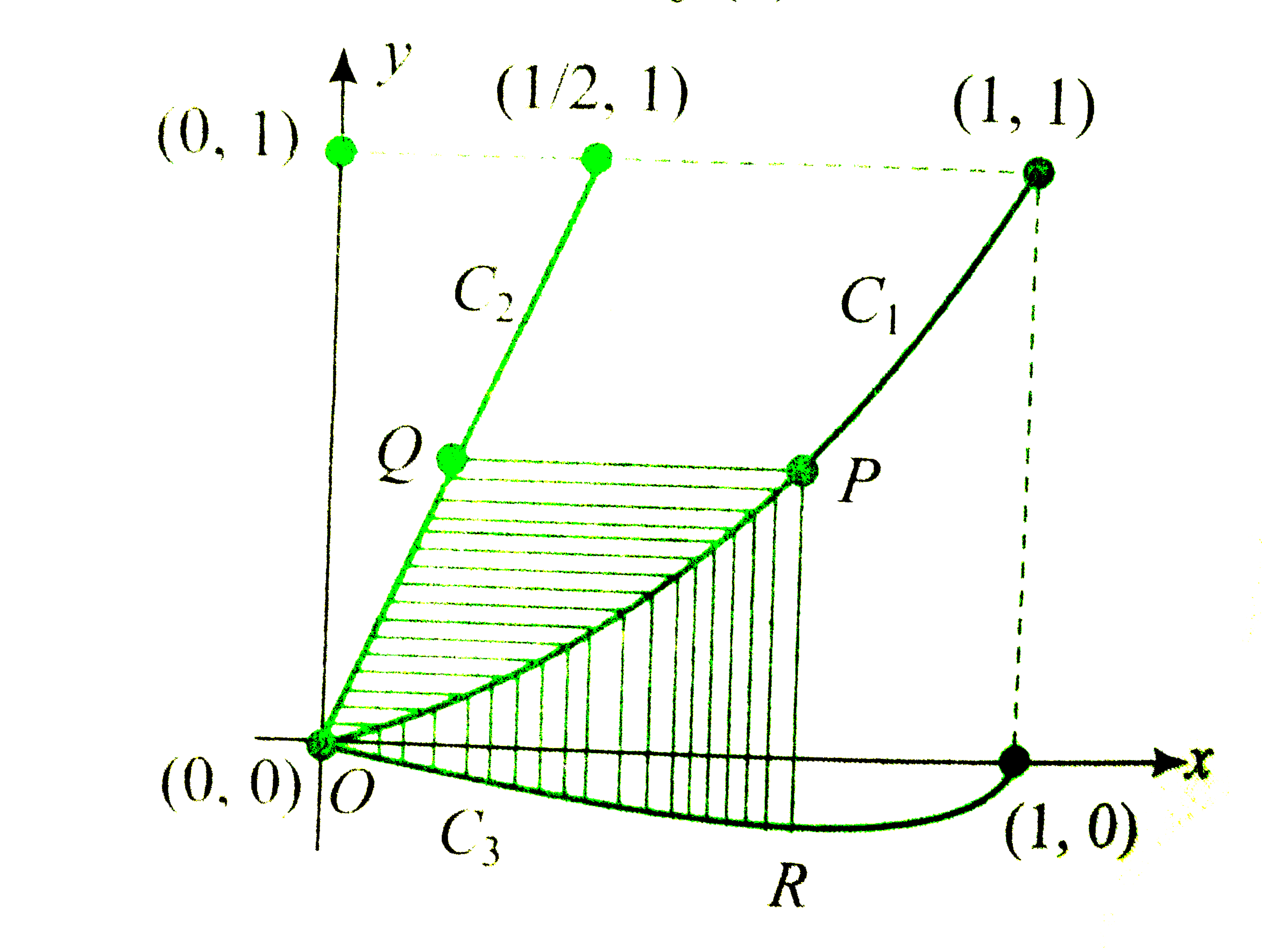
Let $C_{1} and C_{2}$ , be the graph of the functions $y = x^{2} and y = 2 x, 0 \leq x \leq 1$ respectively. Let $C_{3}$ , be the graph of a function $y - (f x), 0 \leq x \leq 1, f (0) = 0$ . For a point Pand $C_{2}$ , let the lines through P, parallel to the axes, meet $C_{2} and C_{3}$ , at Q and R respectively. If for every position of P (on $C_{1}$ ), the areas of the shaded regions $O P Q and O R P$ are equal, determine the function $f (x)$ .

Video Solution

Answer

Step by step video & image solution for Let C_1 and C_2, be the graph of the functions y= x^2 and y= 2x, 0<=x<= 1 respectively. Let C_3, be the graph of a function y- (fx), 0<=x<=1, f(0)=0. For a point Pand C_2, let the lines through P, parallel to the axes, meet C_2 and C_3, at Q and R respectively. If for every position of P (on C_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Knowledge Check

Let $C_{1} and C_{2}$ be the centres of the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0 and x^{2} + y^{2} - 6 x + 14 = 0$ respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral $P C_{1} Q C_{2}$ is:
A8
B6
C9
D4
If the graph of the function $y = {(a - b)}^{2} x^{2} + 2 (a + b - 2 c) x + 1 (\forall a \neq b)$
A $a < b < c$
B $a < c < b$
C $b < a < c$
D $c < b < a$
Let $C_{1} and C_{2}$ be the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ and $x^{2} + y^{2} - 6 x - 6 y + 14 = 0$ respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral $P C_{1} Q C_{2}$ is :
A4
B9
C6
D8

Similar Questions

Knowledge Check

Let $C_{1} and C_{2}$ be the centres of the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0 and x^{2} + y^{2} - 6 x + 14 = 0$ respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral $P C_{1} Q C_{2}$ is:

If the graph of the function $y = {(a - b)}^{2} x^{2} + 2 (a + b - 2 c) x + 1 (\forall a \neq b)$

Let $C_{1} and C_{2}$ be the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ and $x^{2} + y^{2} - 6 x - 6 y + 14 = 0$ respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral $P C_{1} Q C_{2}$ is :

Recommended Questions

Similar Questions

Knowledge Check

Let C1andC2 be the centres of the circles x2+y2−2x−2y−2=0andx2+y2−6x+14=0 respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral PC1QC2 is:

If the graph of the function y=(a−b)2x2+2(a+b−2c)x+1(∀a≠b)

Let C1andC2 be the circles x2+y2−2x−2y−2=0 and x2+y2−6x−6y+14=0 respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral PC1QC2 is :

Recommended Questions

Let $C_{1} and C_{2}$ be the centres of the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0 and x^{2} + y^{2} - 6 x + 14 = 0$ respectively. If P and Q are the points of intersection of these circles, then the area (in sq. units) of the quadrilateral $P C_{1} Q C_{2}$ is:

If the graph of the function $y = {(a - b)}^{2} x^{2} + 2 (a + b - 2 c) x + 1 (\forall a \neq b)$

Let $C_{1} and C_{2}$ be the circles $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ and $x^{2} + y^{2} - 6 x - 6 y + 14 = 0$ respectively. If P and Q are points of intersection of these circles, then the area (in sq. units ) of the quadrilateral $P C_{1} Q C_{2}$ is :