If AD,BEandCF be the median of a △ABC, prove that −−→AD+−−→BE+−−→CF=0
Step by step video & image solution for If AD, BE and CF be the median of a /_\ABC, prove that vec(AD)+vec(BE)+vec(CF)=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
A¯¯¯¯¯¯BD+¯¯¯¯¯¯EA+¯¯¯¯¯¯FBB0C¯¯¯¯¯¯AE+¯¯¯¯¯¯DB+¯¯¯¯¯¯FAD¯0If AD, BE and CF are the medians of a ABC ,then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
A4:3B3:2C3:4D2:3
If AD, BE and CF are medians of triangle ABC then prove that median AD divides line segment EF.
View SolutionIf G is the centroid of a triangle ABC, prove that →GA+→GB+→GC=→0.
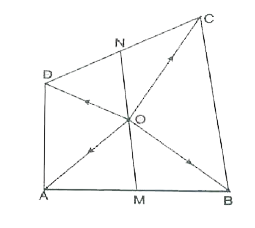
View SolutionIn the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) −−→OA+−−→OB+−−→OC+−−→OD=→0
(ii) −−→BC+−−→AD=2−−−→MN.
View SolutionIf ABCD is quadrilateral and EandF are the mid-points of ACandBD respectively, prove that →AB+→AD +→CB +→CD =4 →EF.
View SolutionIf ABCDEF is a regular hexagon, prove that −−→AC+−−→AD+−−→EA+−−→FA=3−−→AB
View SolutionLet D,EandF be the middle points of the sides BC,CAandAB, respectively of a triangle ABC. Then prove that →AD+→BE+→CF=→0 .
View Solution
