चित्र में, वृत्त कि एक जीवा AB पर लम्ब OD है जहाँ O वृत्त का केन्द्र है | यदि BC एक व्यास है, तो सिद्ध कीजिए कि CA=2OD.
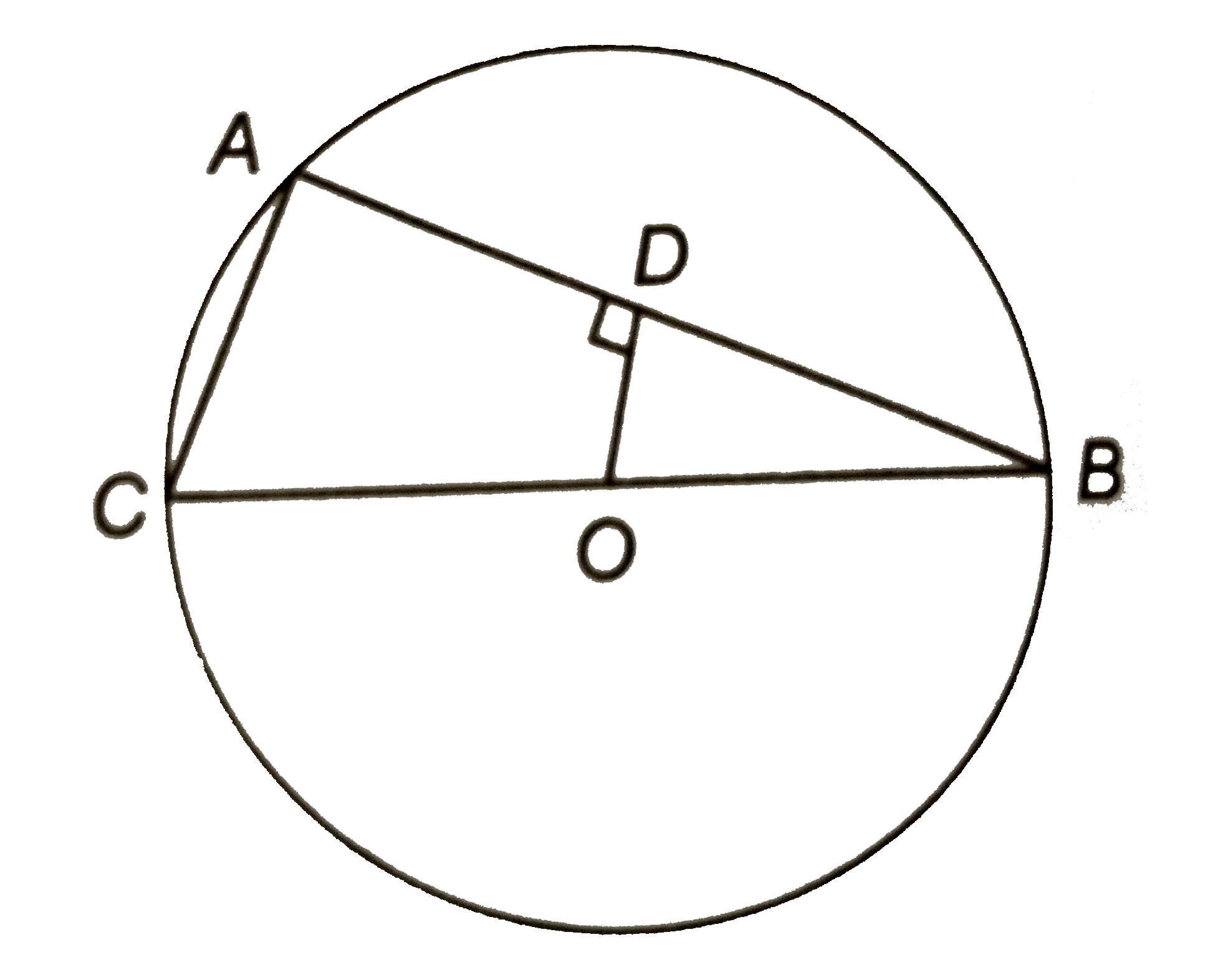
∵OD⊥AB (दिया है) और केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है |
∴D,AB का मध्य बिन्दु है |
तथा O, BC का मध्य बिन्दु है |
अब ΔABC में, D और O क्रमश: AB और BC के मध्य बिन्दु हैं |
∴ OD∣∣AC और OD=1/2 AC
या CA=2OD (मध्य बिन्दु प्रमेय)
Topper's Solved these Questions
- वृत्त Book:NOOTAN HINDIChapter:वृत्त Exercise:प्रश्नावली 10A
Explore 21 Videos
- वृत्त Book:NOOTAN HINDIChapter:वृत्त Exercise:प्रश्नावली 10B
Explore 19 Videos
- रेखाएं और कोण Book:NOOTAN HINDIChapter:रेखाएं और कोण Exercise:दीर्घ उत्तरीय प्रशन
Explore 5 Videos
- संख्या पद्धतिBook:NOOTAN HINDIChapter:संख्या पद्धतिExercise:विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
Explore 10 Videos
Similar Questions
एक वृत्त में 10 सेमी लम्बी जीवा केन्द्र से 12 सेमी कि दूरी पर है | इसी वृत्त के केन्द्र से 5 सेमी की दूरी पर स्थित जीवा की लम्बाई क्या होगी ?
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि ∠ACB=25∘, तो ∠AOB ज्ञात कीजिए |

View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
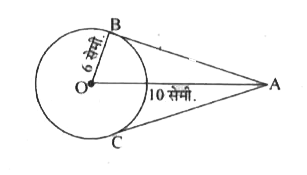
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solution
