एक खिड़की की आकृति एक आयत तथा इस पर बने एक अर्द्धवृत्त की तरह है यदि इसका परिमाप 30 मीटर है तो खिड़की की माप ज्ञात कीजिये जिससे कि इसमें अधिकतम प्रकाश जा सके ।

Video Solution

Text Solution

Verified by Experts

माना ABCDE एक खिड़की है
जिसका परिमाप अचर है ।
माना AE = 2x तथा AB = y
L तथा M क्रमश :AE तथा BD के मध्य बिंदु है ।
तब AL = LE = x
BM = MD = CM = x
दिया है :
खिड़की का परिमाप = 30 मीटर
$\Rightarrow 2 x + 2 y + π x = 30$
$\Rightarrow y = \frac{30 - (2 + π) x}{2}$ .....(1)
यह स्पष्ट है कि खिड़की में जाने वाला प्रकाश अधिकतम होगा
यदि इसका क्षेत्रफल उच्चिष्ठ हो । यदि खिड़की का क्षेत्रफल P है तब
$P = 2 x y + \frac{π x^{2}}{2} = 2 x (\frac{30 - (2 + π) x}{2}) + \frac{π x^{2}}{2}$
$= 30 x - (2 + π) x^{2} + \frac{π x^{2}}{2}$ ...(2)
$\Rightarrow \frac{d P}{d x} = 30 - 2 (2 + π) x + π x = 30 - (4 + π) x$ ....(3)
P के चरम मानों के लिए
$\frac{d P}{d x} = 0$
$\Rightarrow 30 - (4 + π) x = 0$
$\Rightarrow x = \frac{30}{4 + π}$ मीटर
तथा $\frac{d^{2} P}{{d x}^{2}} = - (4 + π) < 0$ (ऋणात्मक संख्या )
$\Rightarrow P$ उच्चिष्ठ होगा , जब $x = \frac{30}{4 + π}$
x का यह मान समीकरण (1) में रखने पर
$y = \frac{30 - (2 + π) \cdot \frac{30}{4 + π}}{2} = \frac{30}{4 + π}$ मीटर
अतः P के उच्चिष्ठ मान के लिए अर्द्धवृत्त की त्रिज्या
$= \frac{30}{4 + π}$ मीटर
तथा $A B = y = \frac{30}{4 + π}$ मीटर
व $A E = \frac{60}{4 + π}$ मीटर

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

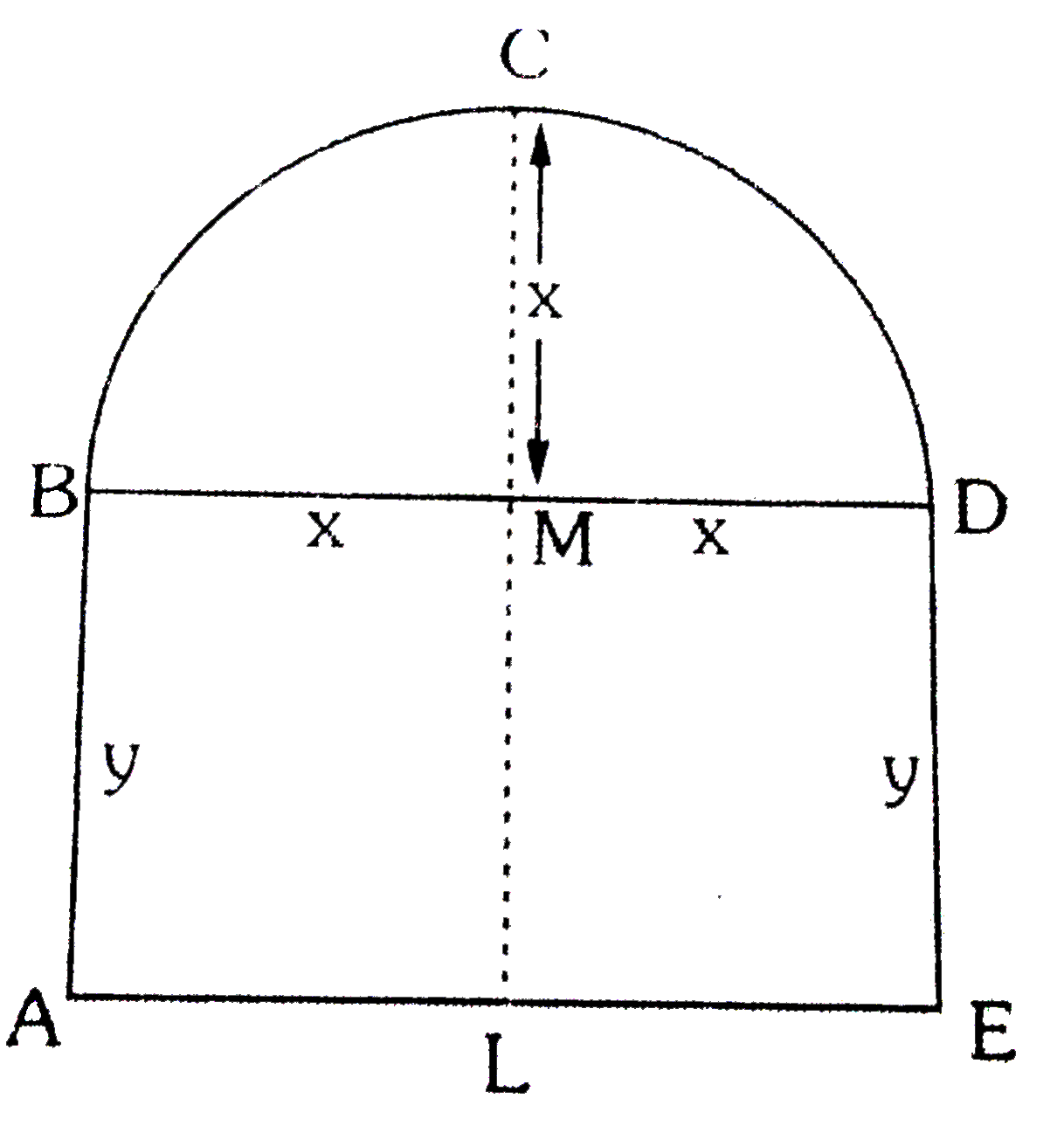
Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-उच्चिष्ठ एवं निम्निष्ठ-विविध उदाहरण

Home
Ask Doubt
Profile