सिद्ध कीजिए कि महत्तम आयतन के उस लंबवृत्तीय शंकु की ऊँचाई जो r त्रिज्या के गोले के अंदर स्थित है ,4r3 है
तथा इस शंकु का अधिकतम आयतन गोले के आयतन के रूप में ज्ञात कीजिए।
माना R शंकु की त्रिज्या तथा h ऊँचाई है जो r त्रिज्या के गोले के अंदर स्थित है ।
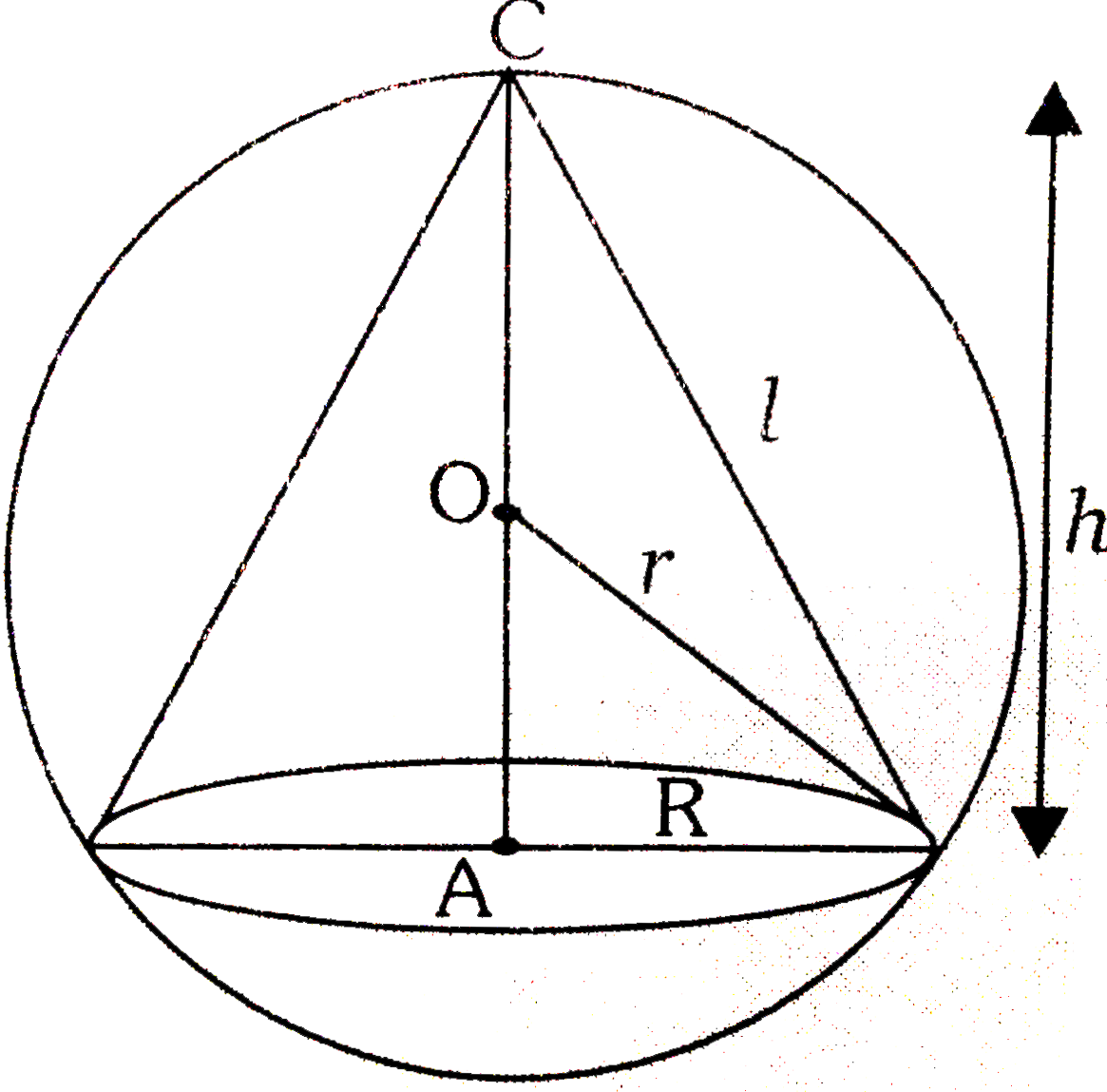
∴OA=h−r
ΔAOB में , पाइथागोरस प्रमेय से -
r2=R2+(h−r)2
⇒r2=R2+h2+r2−2rh
⇒R2=2rh−h2 ...(1)
गोले का आयतन =43πr3
तथा शंकु का आयतन V=13πR2h
⇒V=13πh(2rh−h2) [समीकरण (1) से ]
⇒V=13π(2rh2−h3) ....(2)
समीकरण (2) के दोनों पक्षों को के सापेक्ष अवकलन करने पर -
dVdh=13π(4rh−3h2) ...(3)
अधिकतम तथा न्यूनतम के लिए dVdh=0 रखने पर -
⇒13π(4rh−3h2)=0
⇒4rh=3h2⇒4r=3h
⇒h=4r3 [∵h≠0]
समीकरण (3) के दोनों पक्षों का के सापेक्ष पुनः अवकलन करने पर -
d2Vdh2=13π(4r−6h)
h=4r3पर →(d2Vdh2)h−4r3=13π(4r−6×4r3)
⇒π3(4r−8r)=−4rπ3<0
⇒π3(4r−8r)=−4rπ3<0
⇒h=4r3 पर अधिकतम है ।
समीकरण (2) में h का मान प्रतिस्थापित करने पर -
V=13π[2r(4r3)2−(4r3)3]
=π3[329r3−6427r3]=π3r3[329−6427]
=π3r3[96−6427]=π3r3[3227]
=827×(43πr3)=827×( गोले का आयतन )
अतः शंकु का अधिकतम मान गोले के आयतन का 827 है ।
Topper's Solved these Questions
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.1
18 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.2
14 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - स्वमूल्यांकन परीक्षण
19 Videos
- आव्यूह BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण
17 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
Similar Questions
x के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x
View Solution80 को ऐसे दो भागों में विभाजित कीजिये कि के भाग के घन तथा दूसरे भाग की पाँचवीं घात का गुणनफल महत्तम हो ।
View Solution[0,2π]पर x+sin2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
View Solutionx sin x का समाकलन कीजिए-
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक गुब्बारा जो सदैव गोलाकार रहता है, का व्यास 32(2x+1) है इसके आयतन के परिवर्तन कि दर के सापेक्ष ज्ञात कीजिए।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionउस बड़े से बड़े गोले का आयतन ज्ञात कीजिए, जो उस घन में से काटा गया जिसकी एक भुजा की लम्बाई 4 सेमी है।
View Solutionशंकु एवं गोले का आयतन|उदाहरण
View Solutionगोले एवं अर्ध गोले के आयतन से सम्बंधित प्रश्न
View Solutionशंकु का आयतन|गोले का आयतन#!#अर्धगोले का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|गोले के आयतन पर आधारित महत्वपूर्ण प्रश्न#!#अर्धगोले के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृष्ठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View Solution
