सिद्ध कीजिये कि त्रिज्या R के गोले से उच्चिष्ठ आयतन का जो बेलन काटा जा सकता है , उसकी ऊँचाई $\frac{2 R}{\sqrt{3}}$ है ।
उच्चिष्ठ आयतन भी ज्ञात कीजिये ।

Video Solution

Text Solution

Verified by Experts

माना गोले की त्रिज्या = R
गोले से काटे गये बेलन की ऊँचाई = h
आधार की त्रिज्या = r
OA = R
CA = r
h = $2 \cdot O C$

माना $∠ A O C = θ$
तब $r = C A = R \sin θ$
$O C = R \cos θ \Rightarrow h = 2 R \cos θ$
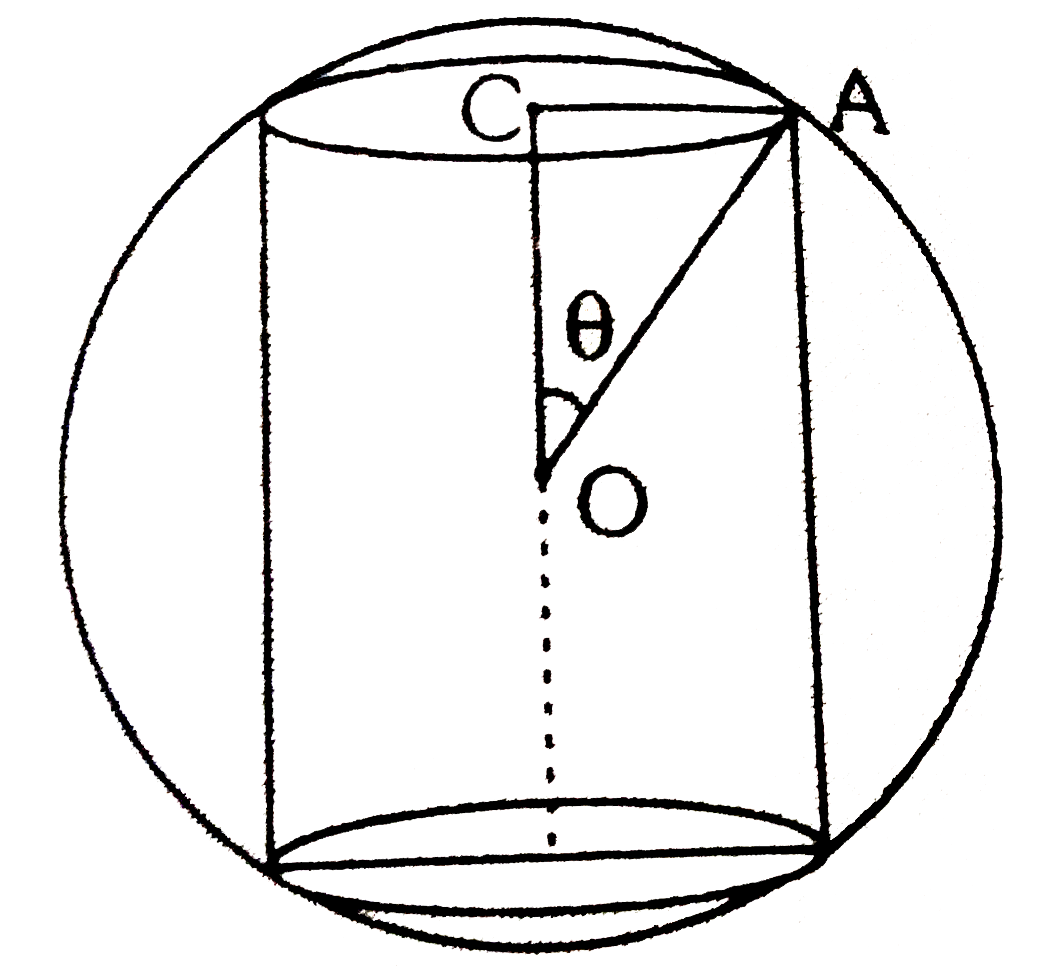
माना बेलन का आयतन V है तब
$V = π r^{2} h$
$= π {(R \sin θ)}^{2} \cdot 2 R \cos θ$
$= 2 π R^{3} \sin^{2} θ \cos θ$ ...(1)
$\frac{d V}{d θ} = 2 π R^{3} (2 \sin θ \cos^{2} θ - \sin^{3} θ)$ ......(2)
व $\frac{d^{2} V}{d θ} = 2 π R^{3} (2 \cos^{3} θ - 7 \sin^{2} θ \cos θ)$ ...(3)
हम जानते है कि V के चरम मानों के लिए

$\frac{d V}{d θ} = 0$
$\Rightarrow \sin θ (2 \cos^{2} θ - \sin^{2} θ) = 0$
$\Rightarrow \tan^{2} θ = 2 \Rightarrow \tan θ = \sqrt{2}$
$∴ \sin θ = \frac{\sqrt{2}}{\sqrt{3}}, \cos θ = \frac{1}{\sqrt{3}}$
$∴ \frac{d^{2} V}{d θ} = 2 π R^{3} (2 \cdot \frac{1}{3 \sqrt{3}} - 7 \cdot \frac{2}{3} \frac{1}{\sqrt{3}}) = \frac{- 8}{\sqrt{3}} π R^{3} < 0$
$∴ V$ का मान उच्चिष्ठ होगा जब $\tan θ = \sqrt{2}$
तथा V का उच्चिष्ठ मान $= 2 π R^{3} {(\frac{\sqrt{2}}{\sqrt{3}})}^{2} (\frac{1}{\sqrt{3}}) = \frac{4 π R^{3}}{3 \sqrt{3}}$
तथा $h = 2 R \cos θ = \frac{2 R}{\sqrt{3}}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-उच्चिष्ठ एवं निम्निष्ठ-विविध उदाहरण

Home
Ask Doubt
Profile