वृत्त $x^{2} + y^{2} = a^{2}$ का क्षेत्रफल ज्ञात कीजिये जबकि a वृत्त की त्रिज्या है |

Video Solution

Text Solution

Verified by Experts

वृत्त का समीकरण $x^{2} + y^{2} = a^{2}$ है जिसकी त्रिज्या a है |यह वक्र x - अक्ष तथा y - अक्ष के परितः सममित है | अक्ष इस वक्र को चार सममित है | अक्ष इस वक्र को चार सममित भागो में विभाजित करते है अतः हम इसके एक भाग ( प्रथम चतुर्थांश में स्थित भाग ) का क्षेत्रफल ज्ञात करके चार से गुणा कर देंगे जिससे हमे वृत्त का क्षेत्रफल प्राप्त हो जाएगा | माना $P (x, y)$ वृत्त पर स्थित $δ x$ चौड़ाई की एक प्रारम्भिक पट्टी ( elementary strip ) है | जिसकी लम्बाई y है | अतः प्रारम्भिक पट्टी PQ का क्षेत्रफल $y δ x$ है | हम वृत्त के चतुर्थांश की इसी प्रकार की प्रारम्भिक पट्टियों में विभाजित कर सकते है | यदि वृत्त का क्षेत्रफल A है, तब वक्र की सममिति के आधार पर अभीष्ट क्षेत्रफल
$A = 4 \int_{0}^{a} y d x = 4 \int_{0}^{a} \sqrt{(a^{2} - x^{2})} d x$

$(∵ x^{2} + y^{2} = a^{2} \Rightarrow y = \sqrt{a^{2} - x^{2}})$
माना $x = a \sin θ \Rightarrow d x = a \cos θ d θ$
सीमाएं $x = 0$ पर $θ = 0$ तथा $x = a$ पर $θ = π / 2$
इसलिए नयी समाकलन सीमाएं $' 0$ से $π / 2'$ है, अतः
$A = 4 \int_{0}^{π / 2} a^{2} \cos^{2} θ d θ$
$= 4 a^{2} \int_{0}^{π / 2} \frac{(1 + \cos 2 θ)}{2} d θ = 2 a^{2} [θ + \frac{\sin θ}{2}] - 0^{π / 2}$
$= 2 a^{2} [(π / 2 + \frac{\sin π}{2}) - (0 + \frac{\sin 0}{2})]$
$= π a^{2}$ वर्ग इकाई

|

Updated on:21/07/2023

Class 12 MATHS INTEGRALS

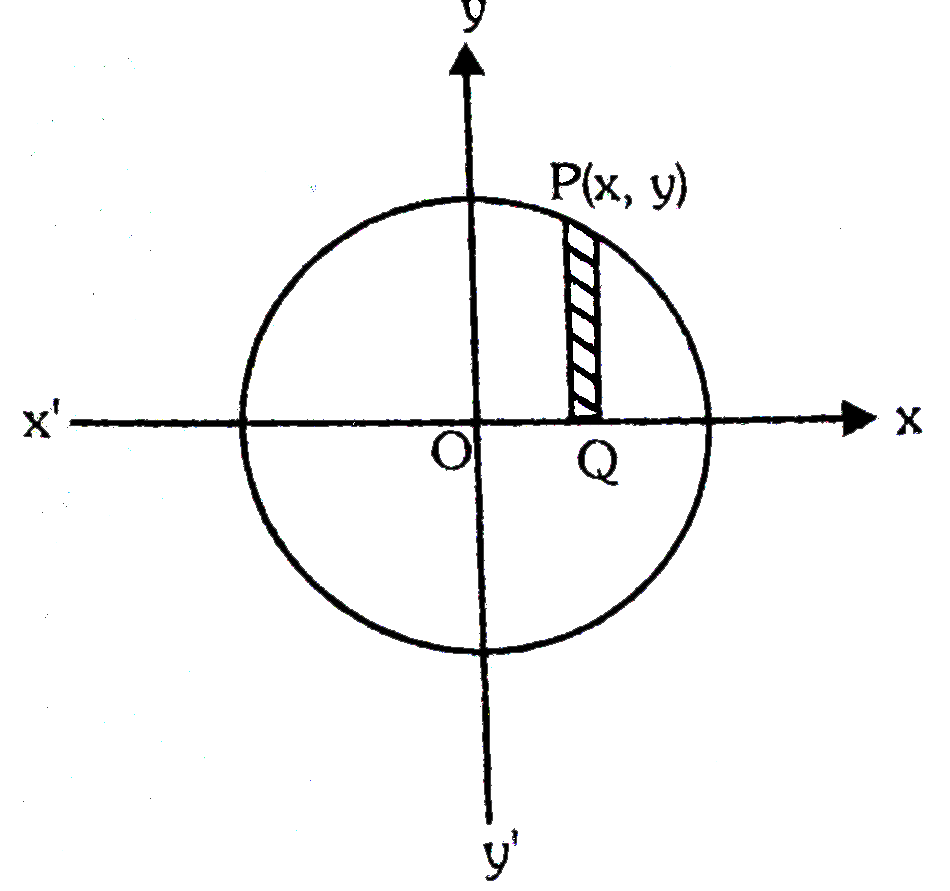
Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-समाकलन के सरल अनुप्रयोग -स्वमूल्यांकन परिक्षण

Home
Ask Doubt
Profile