At the given instan four particle having masses and accleration as shown in the shown in the figure lie at verties of a square. Acceleration on the center of mass of system is : (A) 15(∧i+∧j) (B) 15(∧j+∧i) (C) 15(∧i−∧j) (D) −15(∧i+∧j)
Step by step video & image solution for At the given instan four particle having masses and accleration as shown in the shown in the figure lie at verties of a square. Acceleration on the center of mass of system is : (A) (1)/(5)(overset(wedge)(i) + overset(wedge)(j)) (B) (1)/(5)(overset(wedge)(j) + overset(wedge)(i)) (C) (1)/(5)(overset(wedge)(i) - overset(wedge)(j)) (D) -(1)/(5)(overset(wedge)(i) + overset(wedge)(j)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
In the system shown, the initial acceleration of the wedge of mass 5M is (there is no friction anywhere)
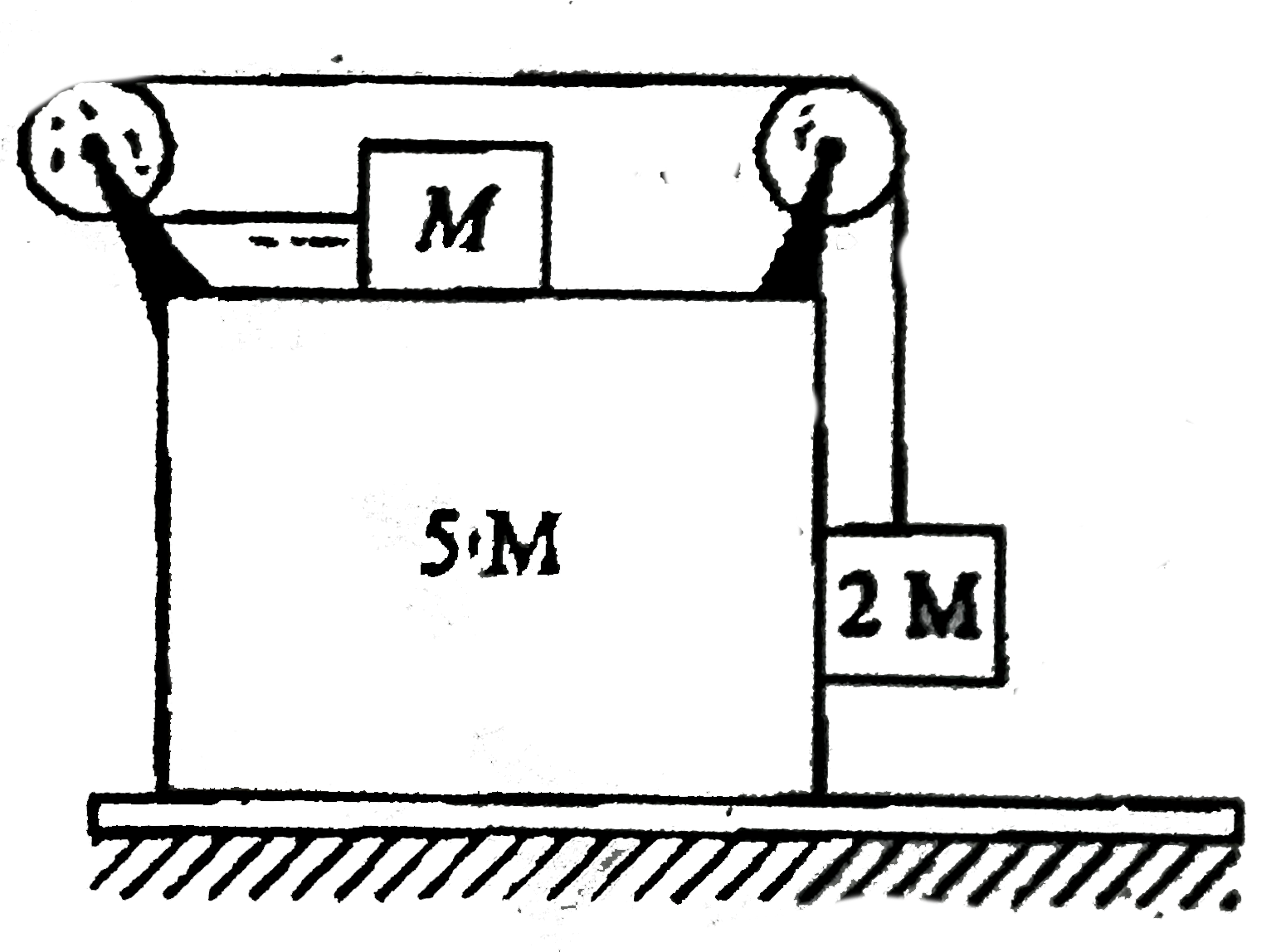 AZeroB2g/23C3g/23DNone
AZeroB2g/23C3g/23DNone - Question 2 - Select One
The triangular wedge shown in the figure is pulled towards left with an acceleration 1.5g. What is the acceleration of m1?
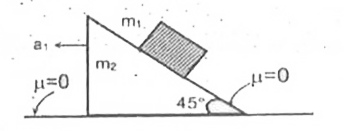 Ag downwardsB1.5 g towards rightC1.5g is vertically downwards directionDNone of the above
Ag downwardsB1.5 g towards rightC1.5g is vertically downwards directionDNone of the above - Question 3 - Select One
In the system shown, the initial acceleration of the wedge of mass 5M is (there is no friction anywhere)
 AzeroBg/2Cg/3Dg/4
AzeroBg/2Cg/3Dg/4
A block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
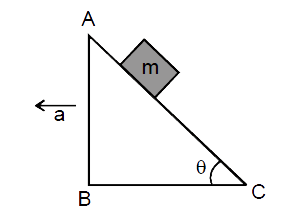 View Solution
View SolutionIf →a=ˆi−ˆk,→b=xˆi+ˆj+(1−x)ˆk and
c=yˆi+xˆj+(1+x−y)ˆk.Then [→a,→b,→c] depends onView SolutionLet →a=ˆi−ˆj,→b−ˆk,→c−ˆk−ˆi. If →d is a unit vector such that →a,Overset(→)(d)=0=[→b→c→d)] then →d equals
View SolutionThe period of small oscillations of a simple pendulum of length l if its point of suspension O moves a with a constant acceleration α=α1∧i−α2∧j with respect to earth is (∧i and ∧j are unit vectors in horizontal in horizontal and vertically upward directions respectively)
View SolutionThe period of small oscillations of a simple pendulum of length l if its point of suspension O moves a with a constant acceleration α=α1∧i−α2∧j with respect to earth is (∧i and ∧j are unit vectors in horizontal in horizontal and vertically upward directions respectively)
View Solution

