ˆi व ˆj क्रमश: x-व y-अक्षो के अनुदिश एकांक सदिश है | सदिशों ˆi+ˆj तथा ˆi−ˆj का परिमाण तथा दिशा क्या होगा ? सदिश →A=2ˆi+3ˆj के ˆi+ˆj व ˆi−ˆj के दिशाओं के अनुदिश घटक निकालिए | [आप ग्राफ़ी विधि की उपयोग कर सकते है | ]
सूत्र सदिश →A=Axˆi+Ayˆj
सदिश →A का परिमाण A=√A2x+A2y ltbRgt यदि यह सदिश x-अक्ष से θ कोण अंतरित करता है, तब
tanθ=(AyAx)
सदिश (ˆi+ˆj) का परिमाण =√(1)2+(1)2=√2
यदि यह सदिश x-अक्ष से θ कोण अंतरित करता है,
tanθ=AyAx=11=1=tan45∘अतः θ=45∘
सदिश (ˆi+ˆj) का परिमाण =√(1)2+(−1)2=√2
यदि यह सदिश (ˆi−ˆj)x-अक्ष से θ कोण अंतरित करती है |
तब
tanθ=(AyAx)=((−1)))1=−1=−tan45∘
θ=−45∘
अतः(ˆi−ˆj) सदिश x-अक्ष से ऋणात्मक दिशा में 45∘ कोण अन्तरित करता है |
सदिश →A=2ˆi+3ˆj का सदिश (ˆi+ˆj) की दिशा में घटक ज्ञात करने के लिए माना →B=(ˆi+ˆj)
सूत्र →A⋅→B=cosθ=(Acosθ)(B)
Acosθ=→A⋅→BB=(2ˆi+3ˆj)⋅(ˆi+ˆj)√(1)2+(1)2
Acosθ=2ˆi⋅ˆi+3ˆj⋅ˆj√2=2+3√2=5√2
[यहाँ ˆi⋅ˆi=ˆj⋅ˆj=ˆk⋅ˆk=1]
सदिश →A=2ˆi+3ˆj का सदिश (ˆi+ˆj) की दिशा में घटक ज्ञात करने के लिए माना →B=ˆi−ˆj.
अतः सदिश →A का सदिश (ˆi−ˆj) के अनुदिश घटक का परिमाण
=(2ˆi+3ˆj)⋅(ˆi−ˆj)∣∣ˆi−ˆj∣∣
=2ˆi⋅ˆi−3ˆj⋅ˆj√(1)2+(−1)2=2−3√2=1√2
अतः √2x−अक्ष से अक्ष से −45∘ पर तथा घटक क्रमशः (5√2,1√2 होंगे |
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिरिक्त प्रश्न
7 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार)
23 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
किसी सदिश में परिमाण व् दिशा दोनों होते है | क्या दीकस्थान में इसकी कोई स्थिति होती है ? क्या यह समय के साथ परिवर्तित हो सकता है | क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों →a व →b का समान भौतिक प्रभाव अवश्य पड़ेगा ? अपने उत्तर के समर्थन में उदाहरण दीजिए |
View Solutionतीन वेक्टर →P,→Q एवं →R चित्र द्वारा दर्शाये गये है | →R वेक्टर पर एक बिंदु S दर्शाया गया है | बिंदु P एवं बिंदु S के बीच विस्थापन b→R है | →P,→Q एवं →S वेक्टर के बीच सम्बन्ध है :
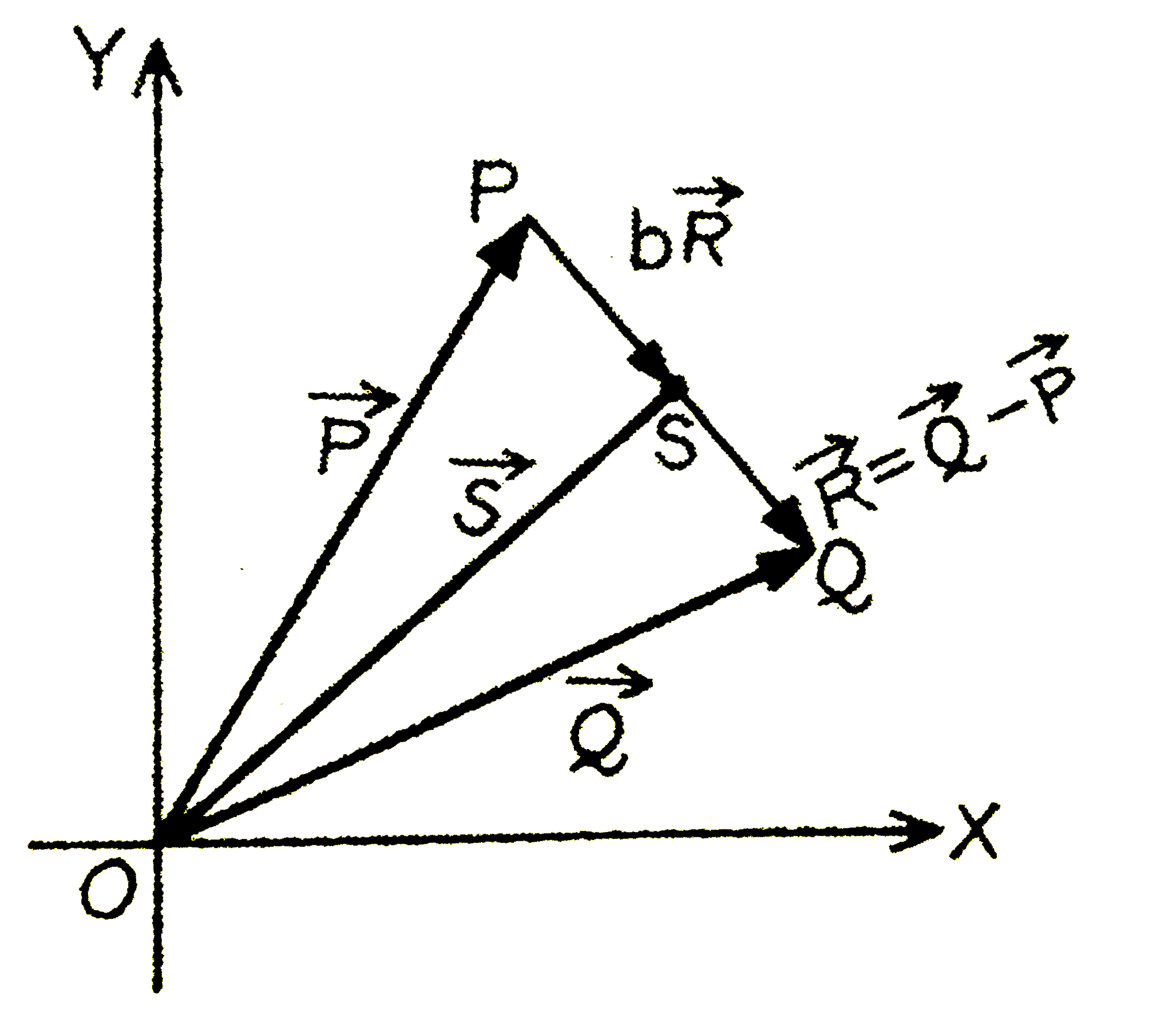
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View SolutionIf →a=ˆi+ˆj,→b=ˆi−ˆj, then →a.→b=
View Solutionयदि →a=ˆi+ˆj−ˆkतथा →b=ˆi−ˆj+ˆkतो →a.→b का मान ज्ञात कीजिए |
View Solutionयदि सदिश 2ˆi+ˆj+ˆk तथाˆi−ˆj+λ लम्बवत है , तब λ=
View Solutionसिद्ध कीजिएः कि [ˆi,ˆj,ˆk]=1व[ˆi,ˆj,ˆk]=−1
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solutionसदिशों →a=2ˆi+4ˆj−5ˆk और →b=λˆi+2ˆj+3ˆk के योग के अनुदिश एकांक सदिश के साथ सदिश ˆi+ˆj+ˆk का अदिश गुणनफल 1 के बराबर होता है। λ का मान ज्ञात कीजिए।
View Solutionसंतालों →r⋅(2ˆi+3ˆj+4ˆk) तथा →r⋅(ˆi+ˆj)=4 के बिच का कोण ज्ञात कीजिए |
View Solutionसदिश 2ˆi−ˆj तथा ˆi+2ˆj के मध्य का कोण ज्ञात कीजिये।
View Solutionसदिश 4ˆi−ˆj+3ˆk तथा −2ˆi+ˆj−2ˆk के लम्बवत 9 इकाई परिमाण वाला सदिश ज्ञात किजिए।
View Solutionसदिश →a=ˆi+2ˆj−3ˆk तथा →b=3ˆi−ˆj+2ˆk दोनो के लम्बवत एक एसा सदिश ज्ञात किजिए, जिसका परिमाण √171 हो।
View Solutionसदिशों (→a−→b) और (→c−→b) दोनों के लंबवत एक मात्रक सदिश ज्ञात कीजिए जहाँ →a=ˆi+2ˆj+ˆk,→b=2ˆi+ˆj तथा →c=3ˆi−4ˆj−ˆk.
View Solution
