दिया है →A+→B+→C+→D=0, निचे दिए गए कथनो में से कौन-सी सही है?
(a) →A,→B,→C तथा →D में से प्रत्यके शून्य सदिश है,
(b) (→A+→C) का परिमाण (→B+→D) के परिमाण के बराबर है,
(c ) →A का परिमाण →B,→C तथा →D के परिमाणों के योग से कभी भी अधिक नहीं हो सकता,
(d) यदि →A तथा →D संरेखीय नहीं है तो →B+→C अवश्य ही →A तथा →D के समतल में होगा, और यह →A तथा →D के अनुदिश होगा यदि वे संरेखीय है |
ऐसा सम्भव है पर इसे ही एक अद्वितीय उत्तर नहीं माना जा सकता, कई अन्य परिस्थितियोँ भी है जिनमे उक्त कथन सत्य हो सकता है | जैसे कि यदि →A+→C=−(→B+→D)|
(b) चूँकि →A+→B+→C+→D=0,
अतः →A+→B=−(→C+→D)
अथवा ∣∣→A+→B∣∣=∣∣→C+→D∣∣
अतः कथन सत्य है |
(c ) चूँकि
→A+→B+→C+→D=0
अतः यह कहा जा सकता हे →A,→V,→C व →D चक्रीय क्रम में एक बहुभुज की भुजाएँ हे या उक्त चारो सदिश मिलकर एक बंद चतुर्भुज बनाते है | अब किसी भी चतुर्भुज में तीन भुजाओं की लम्बाई का योग शेष बची एक भुजा की लम्बाई से सदैव अधिक होता है अतः कथन सत्य है |
(d) चूँकि →A+→B+→C+→D=0 या (→B+→C)+→A+→D=0, अब यदि (→B+→C),→A व →D मिलकर शून्य हो जाते है, तो यह तभी सम्भव हो सकेगा जब (→B+→C),→A व →D एक ही समतल में स्थित हो | अतः (→B+→C),→A व →D के समतल में स्थित है |
पुनः यदि →A व →D संरेखीय नही है, तो →A+(→B+→C)+→D=0
यह तभी सम्भव है जब →A,(→B+→C) व →D मिलकर एक बंद त्रिभुज की रचना करे और इस स्थिति के लिए यह आवश्यक जो जाता है कि →A,(→B+→C) तथा →D एक ही समतल में स्थित हो | परन्तु यदि →A व →D संरेखीय हो, तो सदिश →A+→D व →B+→C को एक ही सरल रेखा के अनुदिश विपरीत दिशाओं होना चाहिए | अतः कथन सत्य है
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिरिक्त प्रश्न
7 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार)
23 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
किसी सदिश में परिमाण व् दिशा दोनों होते है | क्या दीकस्थान में इसकी कोई स्थिति होती है ? क्या यह समय के साथ परिवर्तित हो सकता है | क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों →a व →b का समान भौतिक प्रभाव अवश्य पड़ेगा ? अपने उत्तर के समर्थन में उदाहरण दीजिए |
View Solutionतीन वेक्टर →P,→Q एवं →R चित्र द्वारा दर्शाये गये है | →R वेक्टर पर एक बिंदु S दर्शाया गया है | बिंदु P एवं बिंदु S के बीच विस्थापन b→R है | →P,→Q एवं →S वेक्टर के बीच सम्बन्ध है :
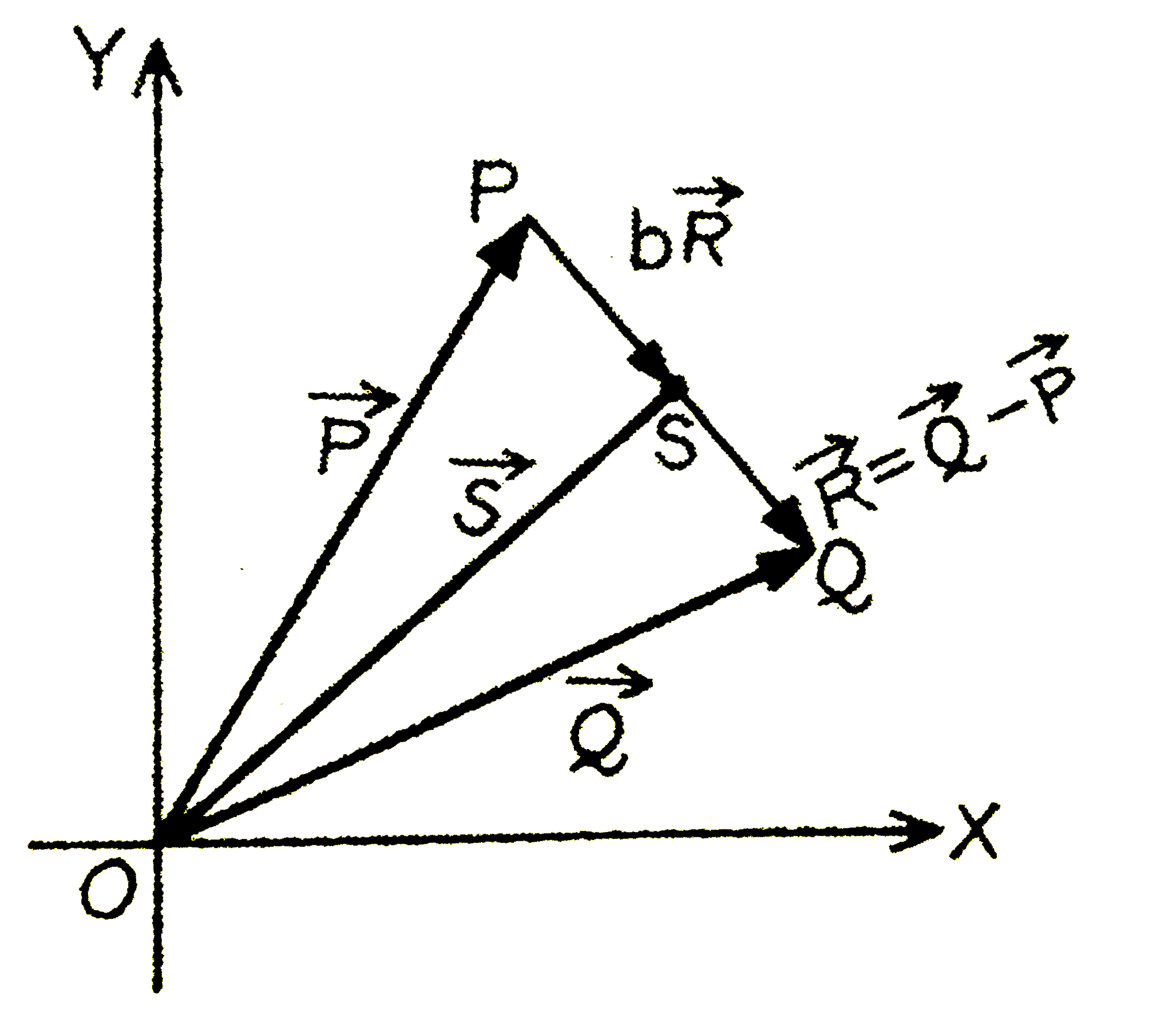
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View SolutionProve that [[veca, vecb + vecc, vecd]] = [[veca, vecb, vecd]] + [[veca, vecc, vecd]]
View SolutionShow that: (→a−→d)×(→b−→c)+(→b−→d)×(→c−→a)+(→c−→d)×(→a−→b) is independent of →d.
View SolutionShow that the points whose position vectors are →a,→b,→c,→d will be coplanar if [→a→b→c]−[→a→b→d]+[→a→c→d]−[→b→c→d]=0
View SolutionIf →a,→b,→c are unity vectors such that →d=λ→a+μ→b+γ→c then gamma is equal to (A) [→a→b→c][→b→a→c] (B) [→b→c→d][→b→c→a] (C) [→b→d→c][→a→b→c] (D) [→c→b→d][→a→b→c]
View Solutionसिद्ध करें कि चार बिंदु स्थिति -सदिश →a,→b,→c और →d हैं , एकतलीय होगें यदि
[→a →b →c]=[→b →c →d]+[→c →a →d]+[→a →b →d]
View SolutionFor any four vectors →a,→b,→c,→d the expressions (→b×→c).(→a×→d)+(→c×→a).(→b×→d)+(→a×→b).(→c×→d)is always equal to:
View SolutionShow that (→a×→b)⋅(→c×→d)+(→b×→c)⋅(→a×→d)+(→c×→a)⋅(→b×→d)=0.
View Solution(→b×→c)⋅(→d×→a)−(→c×→d)⋅(→a×→b)−(→d×→a)⋅(→b×→c)−(→a×→b)⋅(→c×→d) बराबर है
View Solutionयदि सदिश →a,→b तथा →c के लंबवत है, |→a|=2,∣∣→b∣∣=3,|→c|=4 और →b तथा →c के बिच का कोण 2π3 है। तब [→a→b→c] बराबर है
View SolutionFor any four vectors →a , →b , →c , →d we have (→a×→b)×(→c×→d)=[→a,→b,→d]→c−[→a,→b,→c]→d=[→a,→c,→d]→b−[→b,→c,→d]→a .
View SolutionIF →A×→B=→C×→Dand→A×→C=→B×→D+ while ∣∣→A∣∣≠∣∣→D∣∣∣∣→B∣∣≠∣∣→C∣∣ show (→A−→D) that and (→B−→C) are parallel
View SolutionFor any four vectors, prove that (→a×→b)×(→c×→d)=[→a→c→d]→b−[→b→c→d]→a
View Solution
