निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए :
(a) ∣∣→A+→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
(b) ∣∣→A+→B∣∣≥∣∣∣∣→A∣∣−∣∣→B∣∣∣
(c ) ∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
∣∣→A−→B∣∣≥∣∣∣∣→A∣∣−∣∣→B∣∣∣
इनमे समिका (समता) का चिन्ह कब लागू होता है ?
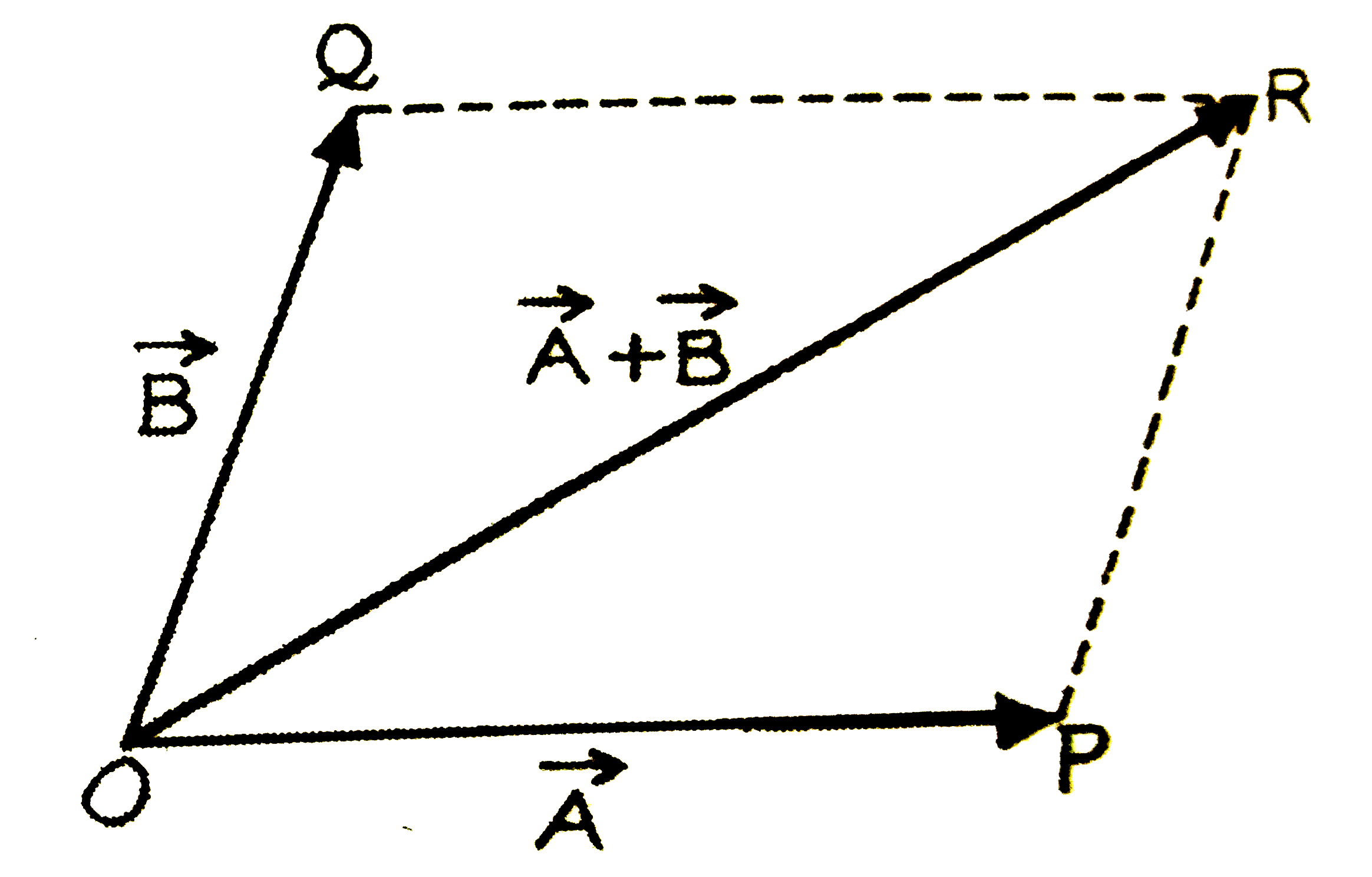
माना सदिश →A व →B संग्लन समानांतर चतुर्भुज OPRQ की भुजाओं OP तथा OQ से प्रदर्शित किये जा सकते है | अब सदिशों के संयोजन के समानांतर चतुर्भुज नियम से इनका परिणामो →A+→B चतुर्भुज एक विकर्ण OR से व्यक्त किया जा सकता है, जैसा कि संलग्न चित्र से स्पष्ट है |
अतः OP∣∣→A∣∣,OQ=PR=∣∣→B∣∣
तथा OR=∣∣→A+→B∣∣
(a) ∣∣→A+→B∣∣≤∣∣→A∣∣+∣∣→B∣∣ का सत्यापन:
(a) ∣∣→A+→B∣∣≤∣∣→A∣∣+∣∣→B∣∣ जैसा कि ज्ञात कि किसी त्रिभुज कि किसी भी भुजा कि लम्बाई अन्य दो भुजाओं कि लम्बाई के योग से सर्वथा कम होती है |
अतः त्रिभुज OPR में,
OR<OP+PR अथवा OR<OP+OQ
अथवा ∣∣→A+→B∣∣<∣∣→A∣∣+∣∣→B∣∣ ...(i)
अब यदि सदिश →A व →B एक ही सरल रेखा के अनुदिश कार्य करते हुए एक ही दिशा में दिष्ट हो, तो
∣∣→A+→B∣∣=∣∣→A∣∣+∣∣→B∣∣ ...(ii)
असमता एवं संता शर्तो [समीकरण (i) व (ii)]
∣∣→A+→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
(b) ∣∣→A+→B∣∣<∣∣→A∣∣−∣∣→B∣∣ का सत्यापन:
त्रिभुज OPR में,
OR+PR>OP अथवा OR>OP−PR
अथवा ∣∣→A+→B∣∣>∣∣→A∣∣−∣∣→B∣∣ ...(iii)
अब यदि सदिश →A तथा →B एक ही रेखा के अनुदिश विपरीत दिशाओं में कार्यरत हो, तब
∣∣→A+→B∣∣=∣∣→A∣∣−∣∣→B∣∣ ...(iv)
समीकरण (iii) व (iv) कि असमिकाओं एवं समिकाओं का संयोग करने पर,
∣∣→A+→B∣∣≥∣∣→A∣∣−∣∣→B∣∣
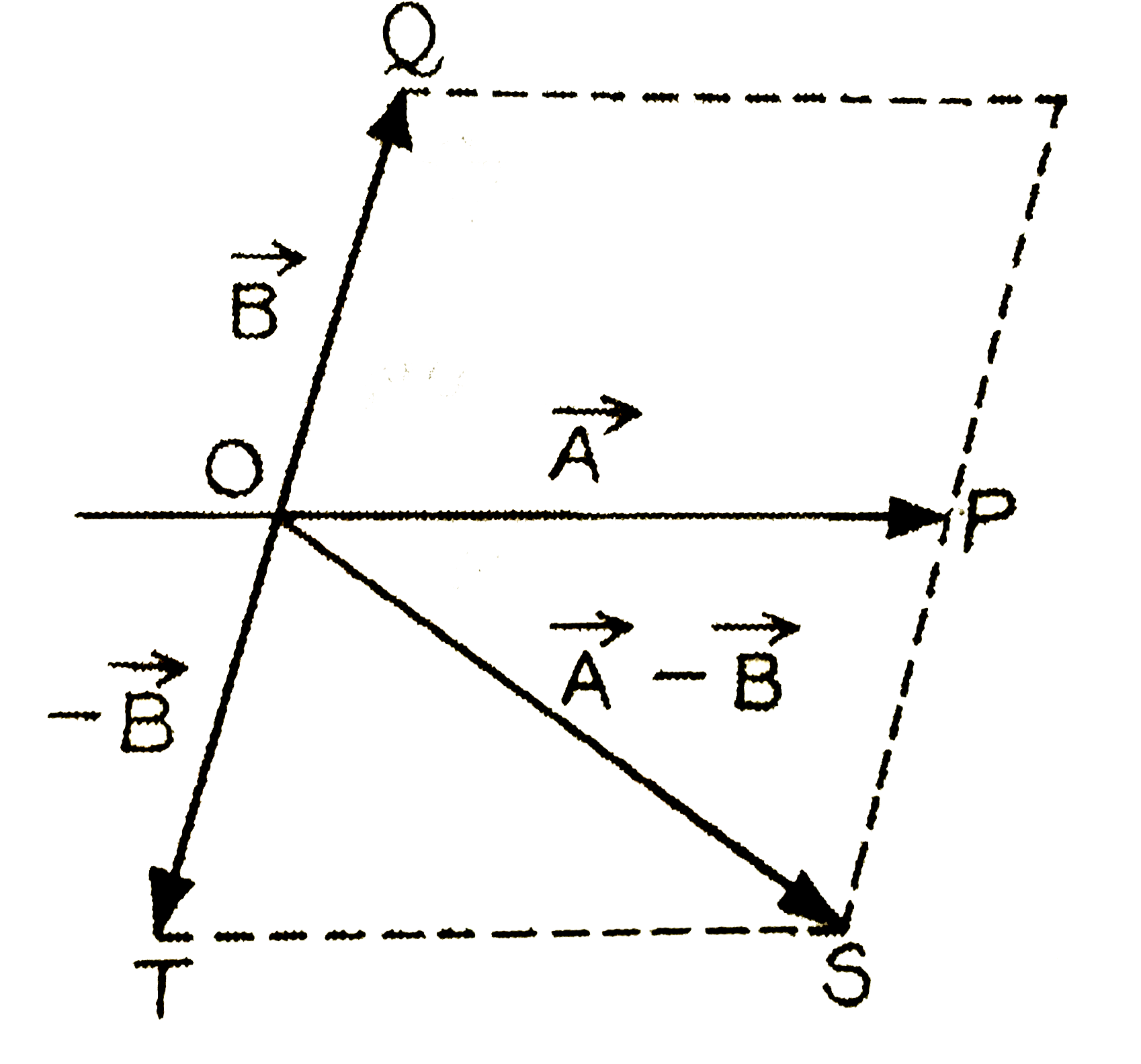
(c ) ∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣ का सत्यापन:
माना सदिश →A व →B संलग्न चित्र में दिखाये गये समानांतर चतुर्भुज कि आसन्न भुआजों क्रमश: OP तथा OQ से निरूपित है | अतः (−→B) OT जो कि परिमाण में OQ के बराबर एवं दिशा में विपरीत है, के द्वारा निरूपित किया जा सकता है | अतः सदिशों के योग के समानांतर चतुर्भुज नियम से सदिश →A तथा →B का परिणामी →A−→B समांतर चतुर्भुज OPST के विकर्ण OS से निरूपित होगा | अब △OPS में,
OS<OP+PS अथवा OS<OP+OT
अथवा ∣∣→A−→B∣∣<∣∣→A∣∣+∣∣−→B∣∣
अथवा ∣∣→A−→B∣∣<∣∣→A∣∣+∣∣→B∣∣ ...(v)
अब यदि सदिश →A एवं →B एक ही सरल रेखा के अनुदिश विपरीत दिशाओं में कार्यरत हो, तब
∣∣→A−→B∣∣=∣∣→A∣∣+∣∣→B∣∣ ...(vi)
समीकरण (v) एवं (vi) का संयोजन करने पर,
∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
(d) ∣∣→A−→B∣∣≥∣∣→A∣∣−∣∣→B∣∣ का सत्यापन :
त्रिभुज OPS में, OS+PS>OP अथवा OS>OP−PS
अथवा ∣∣→A−→B∣∣>∣∣→A∣∣−∣∣−→B∣∣
अथवा ∣∣→A−→B∣∣>∣∣→A∣∣−∣∣→B∣∣ ...(vii)
अब यदि →A व →B सदिश एक ही सरल रेखा के अनुदिश एक ही दिशा में दिष्ट हो, तब
∣∣→A−veB∣∣=∣∣→A∣∣−∣∣→B∣∣ ...(viii)
समीकरण (vii) व (viii) से प्राप्त शर्तो को संयुक्त रूप से लिखने पर,
∣∣→A−→B∣∣≥∣∣→A∣∣−∣∣→B∣∣
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिरिक्त प्रश्न
7 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार)
23 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
किसी सदिश में परिमाण व् दिशा दोनों होते है | क्या दीकस्थान में इसकी कोई स्थिति होती है ? क्या यह समय के साथ परिवर्तित हो सकता है | क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों →a व →b का समान भौतिक प्रभाव अवश्य पड़ेगा ? अपने उत्तर के समर्थन में उदाहरण दीजिए |
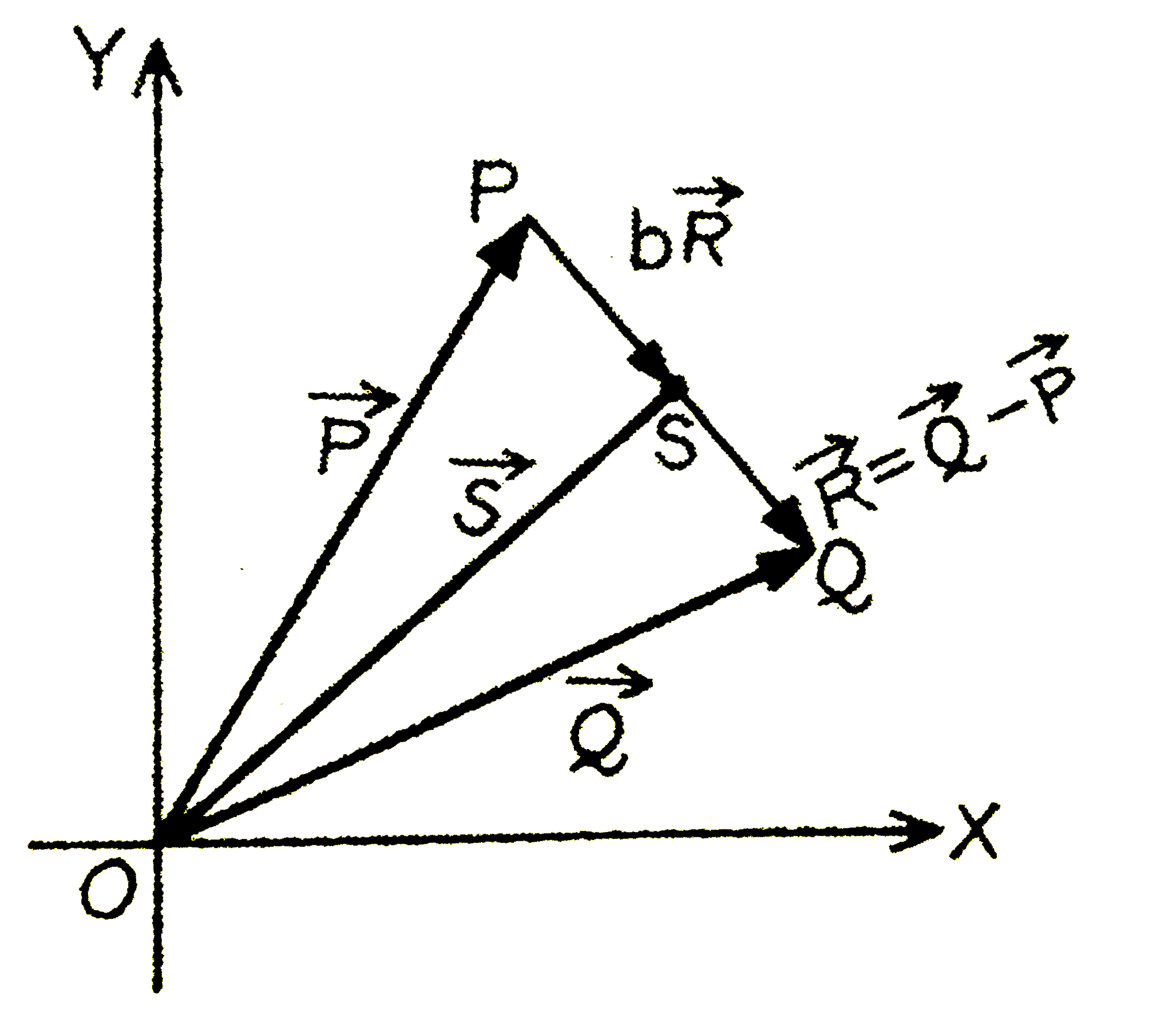
View Solutionतीन वेक्टर →P,→Q एवं →R चित्र द्वारा दर्शाये गये है | →R वेक्टर पर एक बिंदु S दर्शाया गया है | बिंदु P एवं बिंदु S के बीच विस्थापन b→R है | →P,→Q एवं →S वेक्टर के बीच सम्बन्ध है :
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View Solutionदर्शाइए कि दो सदिशों →a ओर →b के लिए |→a|→b+∣∣→b∣∣→a , |→a|→b−∣∣→b∣∣→a, परस्पर लम्बवत हैं
View SolutionProve that ∣∣→a×→b∣∣2=∣∣∣→a⋅→a→a⋅→b→a⋅→b→b⋅→b∣∣∣.
View Solutionदर्शाइए कि दो शून्येतर सदिशों →a और →b के लिए |→a|→b+∣∣→b∣∣→a,|→a|→b|−|→b∣→a पर लंब है।
View SolutionIf |→a|=∣∣→b∣∣, then (→a+→b).(→a−→b) is equal to
View Solutionसदिशों तथा के लिए सिद्ध कीजिए कि
∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→a.→b→a.→b∣∣∣
View Solutionदर्शाइए कि दो शून्येतर सदिशों →a और →b के लिए |→a|→b+∣∣→b∣∣→a,|→a|→b−∣∣→b∣∣→a पर लम्ब है ।
View SolutionIf (→a+→b).(→a−→b)=8and|→a|=8(→b) then find ∣∣→b∣∣.
View SolutionFind ∣∣→b∣∣,if (→a+→b).(→a−→b)=8 and |→a|=8∣∣→b∣∣.
View Solutionप्रक्कथनः यदि़ ∣∣→A+→B∣∣=∣∣→A−→B∣∣ हो तो →A तथा →B के बीच का कोण 90∘ होगा।
कारणः →A+→B=→B+→A
View SolutionFind ∣∣→b∣∣ if (→a+→b).(→a−→b)=8 and |→a|=8∣∣→b∣∣
View SolutionFind ∣∣→b∣∣ if (→a+→b).(→a−→b)=8and|→a|=8∣∣→b∣∣
View Solution
