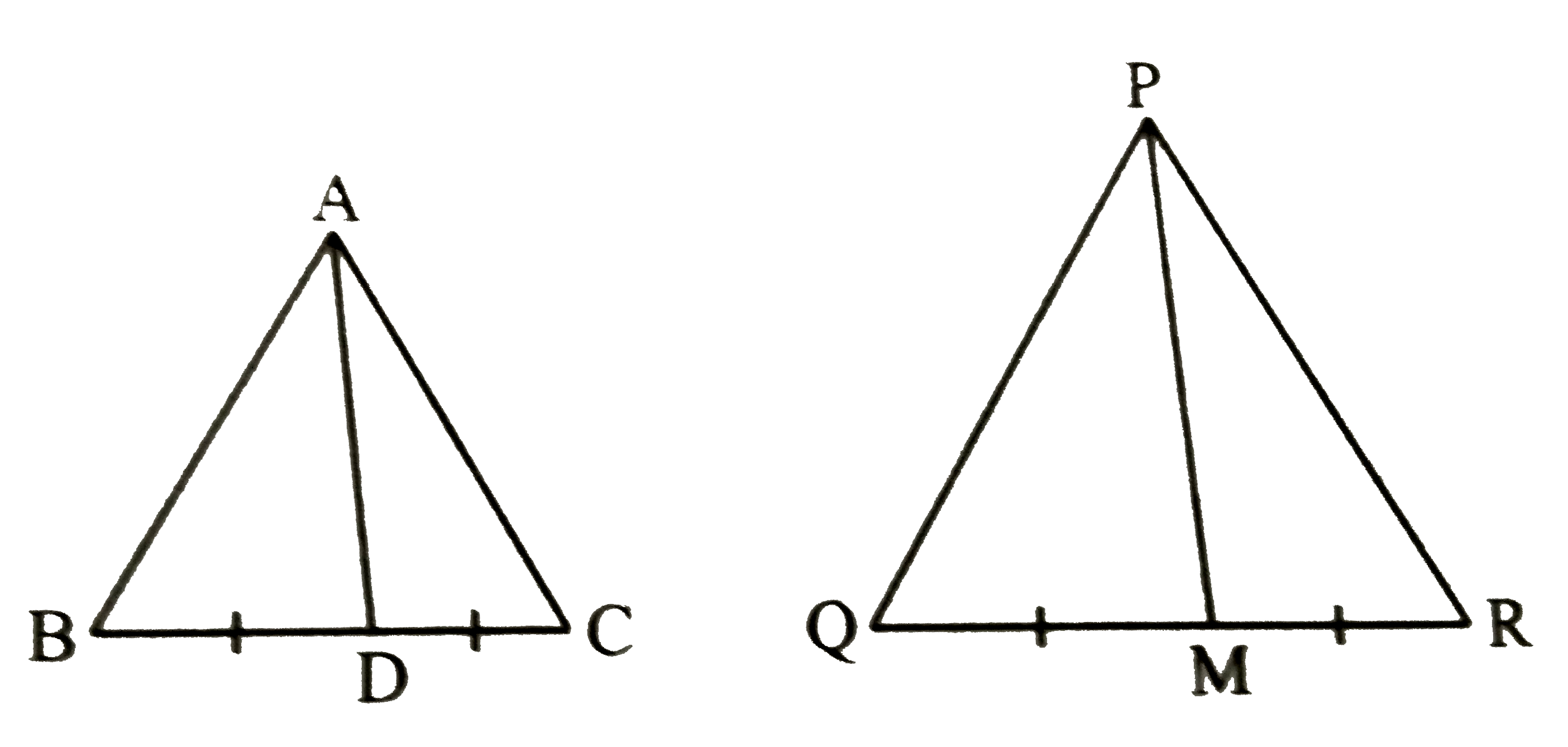
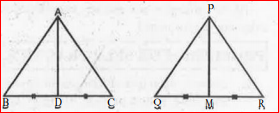
यदि AD तथा PM क्रमशः △ABC तथा △PQR के समद्विभाजक है जहाँ △ABC~△PQR है तो सिद्ध कीजिए कि :
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
माना △ABC तथा △PQR दो समरूप त्रिभुज है
तथा इनके मध्यम AD तथा PM है |
⇒△ABC~△PQR
चूँकि △ABC~△PQR
⇒∠B=∠Q (1)
तथा ABPQ=ACPR=BCQE ...(2)
किन्तु चूँकि D तथा M क्रमशः तथा के मध्य बिंदु है |
इसलिए, BCQR=2BD2QM=BDQM
(i) △ABD तथा △PQM में,
ABPQ=BDQM तथा ∠B=∠Q
तब समरूपता की SAS-कसौटी द्वारा,
△ABD~△PQM
इसलिए आधारभूत समानुपातिक प्रमेय द्वारा,
ABPQ=(AD)(PM)
(iii) चूँकि △ABD~△PQM
इसलिए, ∠ADB=∠PMQ
⇒180∘−∠ADB=180∘−∠PMQ
अतः ∠ADC=∠PMR
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
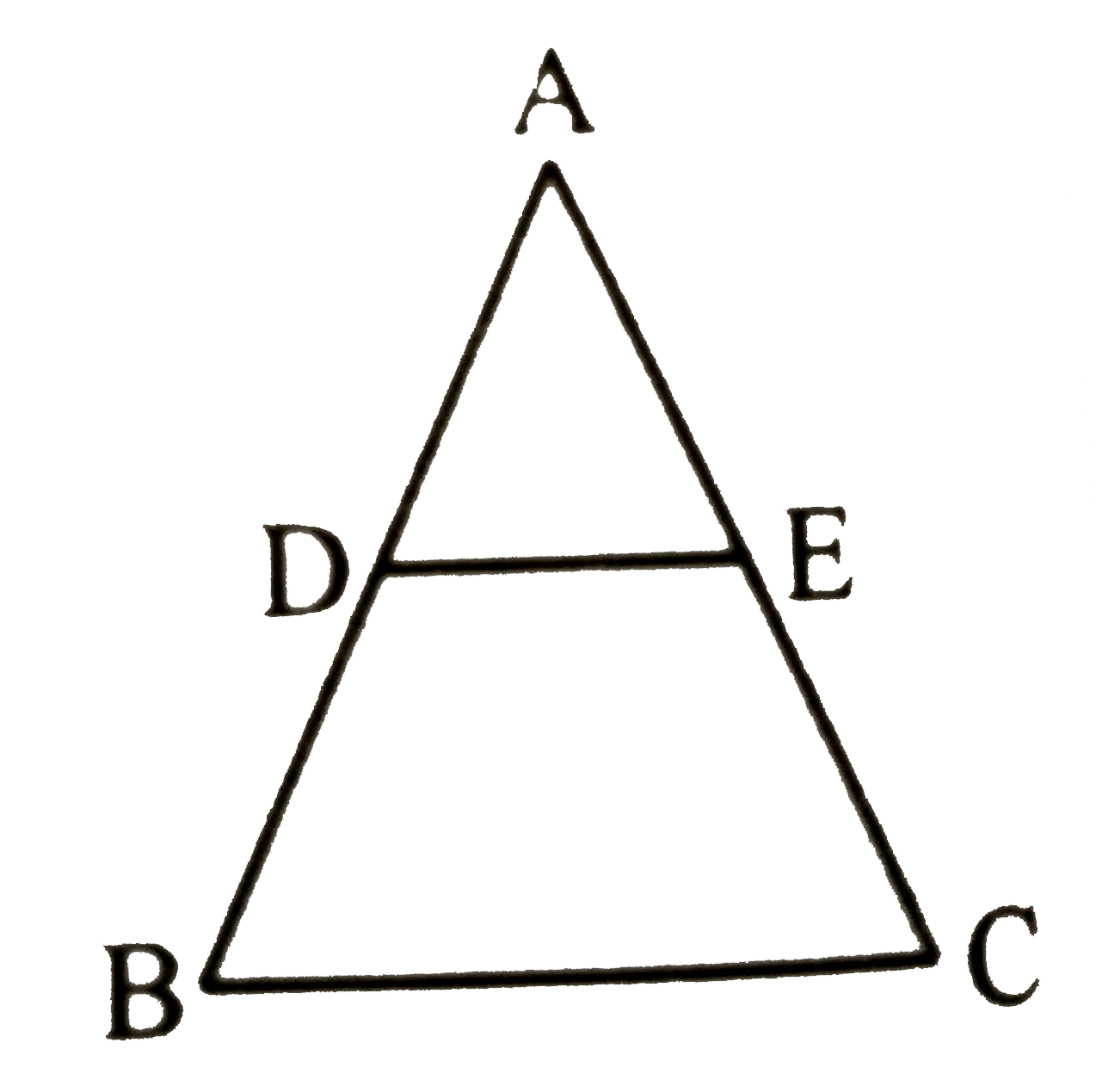
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionAD और PM त्रिभुजों ABC और PQR कि क्रमशः मध्यिकाएँ है जबकि ΔABC~ΔPQR है सिद्ध कीजिए कि ABPQ=ADPM है
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
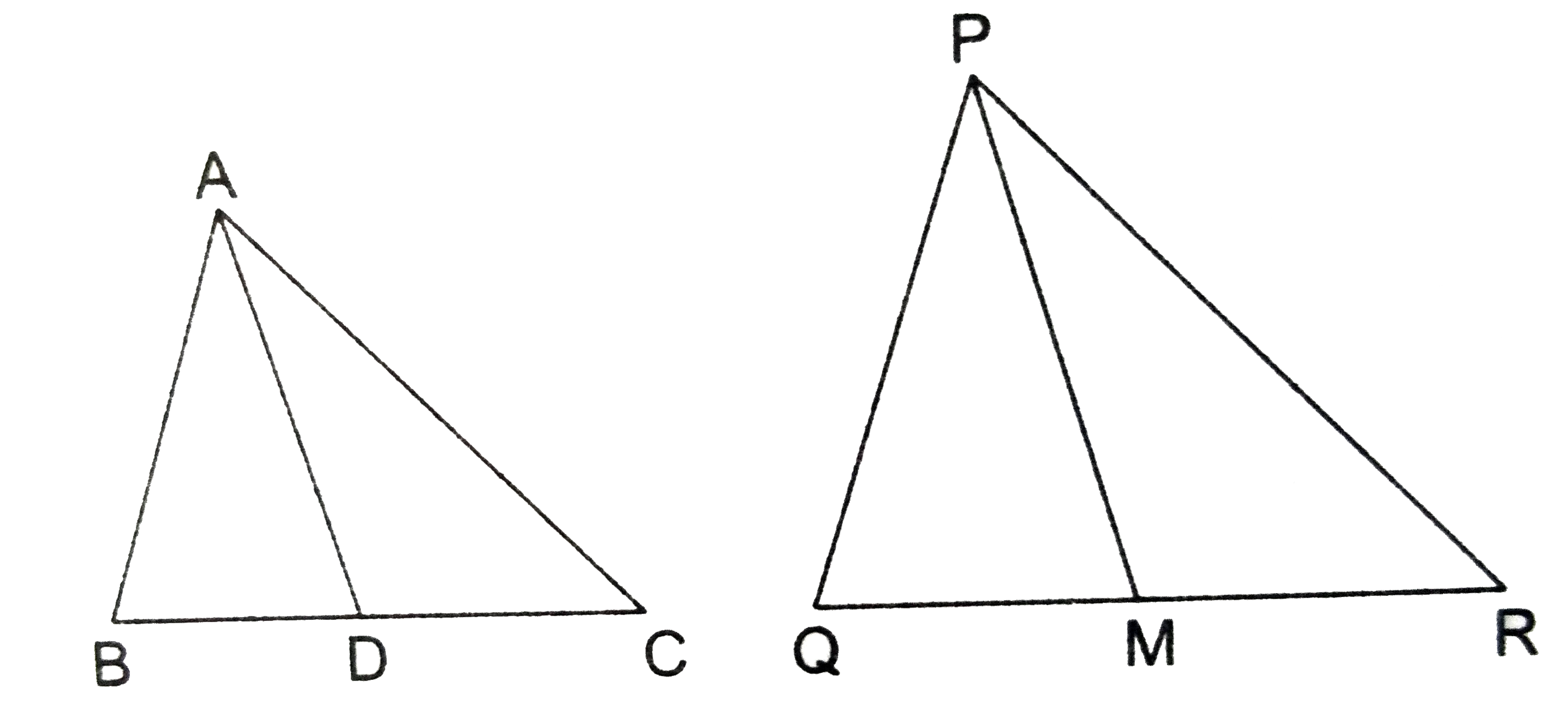
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View Solutionयदि AD और PM ΔABCऔरΔPQR की क्रमशः मध्यिकाएँ है , और जहाँ ΔABC~ΔPQR सिद्ध करें कि
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
View SolutionIf Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIf AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
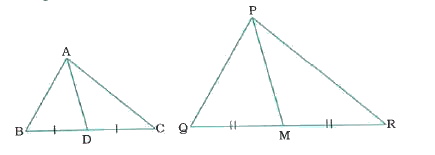
View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively where △ABC~△PQR , Prove that ABPQ=ADPM .
 .
.
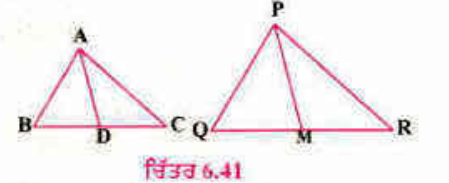
View Solutionਇੱਕ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ AB ਅਤੇ BC ਮੱਧਿਕਾ AD ਕਿਸੇ ਹੋਰ ਤ੍ਰਿਭੁਜ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਭੁਜਾਵਾਂ PQ,QR ਅਤੇ ਮੱਧਿਕਾ PM ਦੇ ਸਮਾਨ-ਅਨੁਪਾਤੀ ਹਨ(ਦੇਖੋ ਚਿੱਤਰ 6.41)।ਦਿਖਾਉ ਕਿ ΔABC~ΔPQR ਹੈ।
View SolutionAD ਅਤੇ PM ਤ੍ਰਿਭੁਜਾਂ ABC ਅਤੇ PQR ਦੀਆਂ ਕ੍ਰਮਵਾਰ ਮੱਧਿਕਾਵਾਂ ਹਨ, ਜਦੋਂ ਕਿ ΔABC~ΔPQR ਹੈ।ਸਿੱਧ ਕਰੋ ਕਿ ABPQ=ADPM ਹੈ।
View Solution
