माना एक चतुर्भुज ABCD है तो सिद्ध कीजिए कि AB2+BC2+CD2+DA2=AC2+BD2
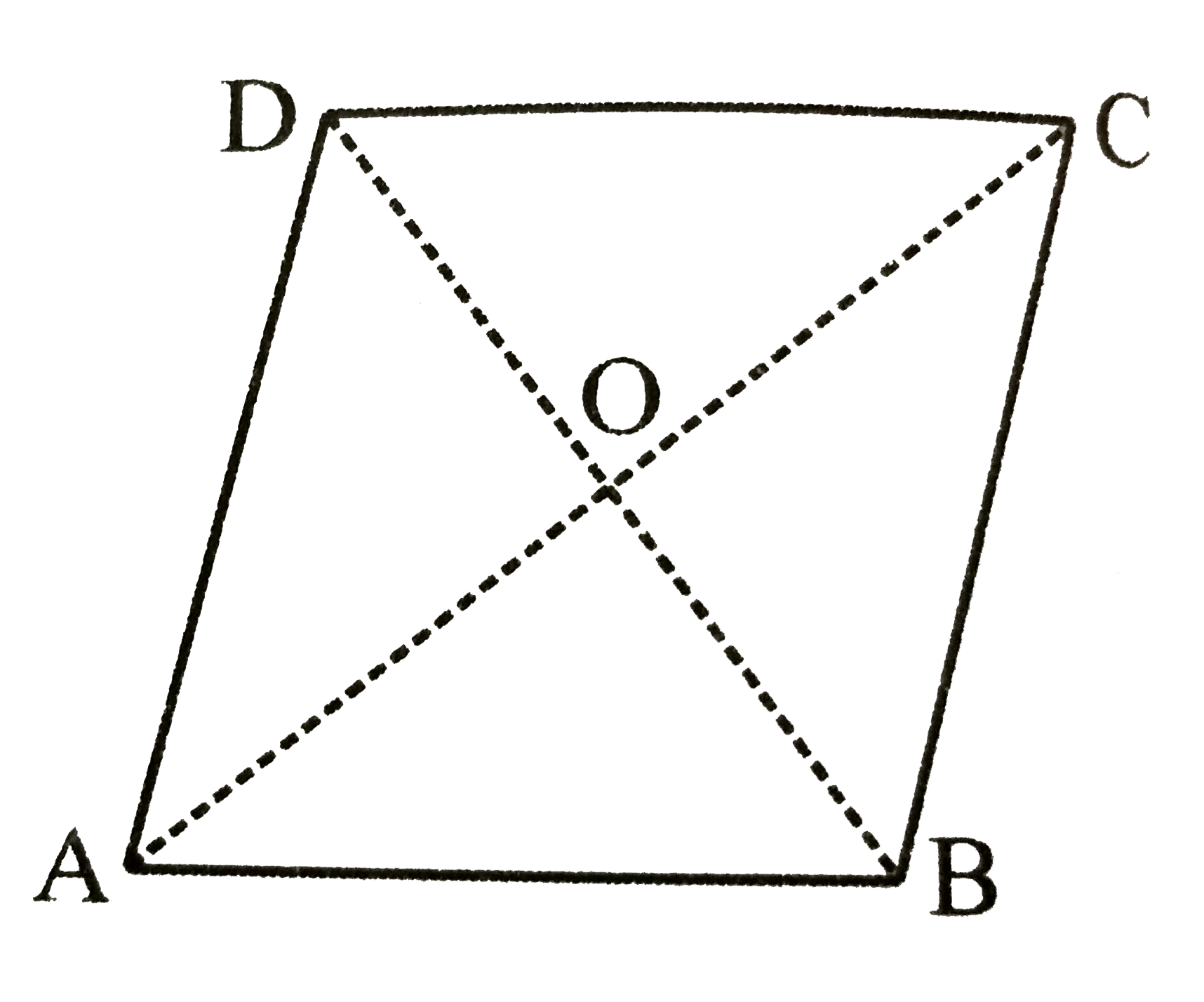
यहाँ एक समचतुर्भुज ABCD है तथा इसका विकर्ण AC व BD बिन्दु O पर प्रतिच्छेद करते है हम जानते है कि एक समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते है इसलिए यहाँ,
∠AOB=∠BOC=∠COD=∠DOA=90∘
तथा AO=CO,BO=OD ...(1)
△AOB में पाइथागोरस प्रमेय से,
AB2=OA2+OB2
⇒AB2=(12AC)2+(12BD)2 [समी० (1) से]
⇒4AB2=AC2+BD2 ...(2)
इसी प्रकार हम दिखा सकते है कि
4BC2=AC2+BD2 ...(3)
4CD2=AC2+BD2 ...(4)
तथा 4AD2=AC2+BD2 ..(5)
(2), (3), (4) तथा (5) को जोड़ने पर,
4(AB2+BC2+CD2+AD2)=4(AC2+BD2)
अतः AB2+BC2+CD2+AD2=AC2+BD2
Topper's Solved these Questions
- त्रिभुज Book:BALAJI PUBLICATIONChapter:त्रिभुज Exercise:अभ्यास प्रश्न 7.1
Explore 9 Videos
- त्रिभुज Book:BALAJI PUBLICATIONChapter:त्रिभुज Exercise:अभ्यास प्रश्न 7.2
Explore 17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ Book:BALAJI PUBLICATIONChapter:त्रिकोणमितीय अनुपात एव असमिकाएँ Exercise:स्वमूल्यांकन परीक्षण
Explore 35 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:BALAJI PUBLICATIONChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:स्वमूल्यांकन परीक्षण
Explore 29 Videos
Similar Questions
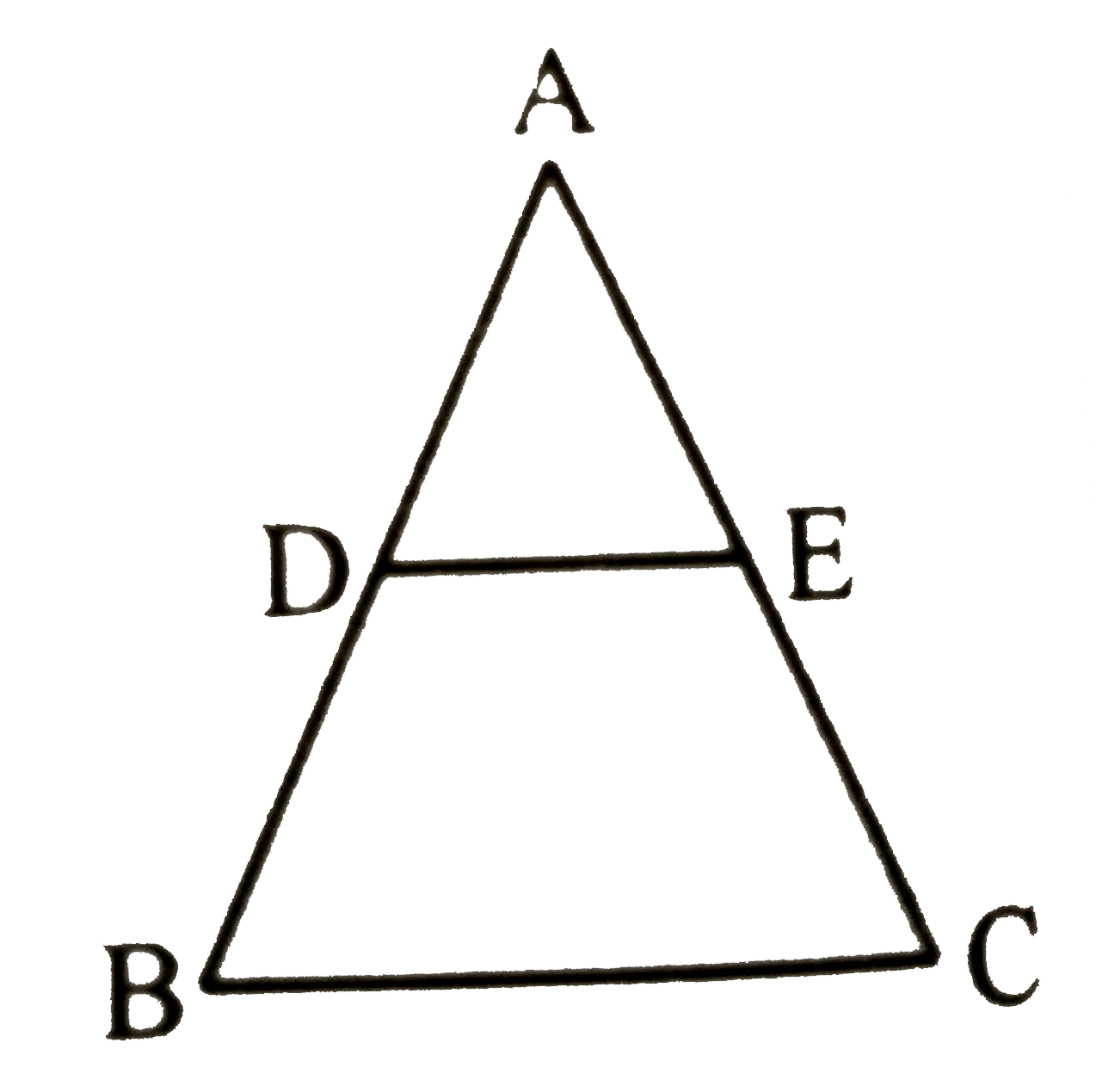
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionIn a quadrilateral ABCD, prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2, where P and Q are middle points of diagonals AC and BD.
View SolutionABCD is a rhombus. Prove that AB2+BC2+CD2+DA2=AC2+BD2
View SolutionIn a quadrilateral ABCD prove that AB2+BC2+CD2+DA2=AC2+BD2+4PQ2 where P and Q are middle points of diagonals AC and BD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionShow that in a quandrilateral ABCD,AB+BC+CD+DA<2(BD+AC).
View SolutionABCD एक समचतुर्भुज है । सिद्ध कीजिए कि AB2+BC2+CD2+DA2=AC2+BD2.
View Solutionयदि ABCD एक चतुर्भुर्ज है जिसके विकर्ण AC और BD,O पर परिच्छेद करते है तो सिद्ध कीजिए की :
(i)(AB+BC+CD+DA)>(AC+BD)
(ii) (AB+BC+CD+DA)<2(AC+BD)

View SolutionABCD is a rhombus.Prove that AB2+BC2+CD2+DA2=AC2+BD2
View Solutionयदि a:b=c:d हो, तो सिद्ध कीजिए कि
a2+ab+b2c2+cd+d2=a2−ab+b2c2−cd+d2
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View Solution
