व्याख्या कीजिए कि भिन्न - भिन्न तापों व के दो पिण्डों को यदि ऊष्मीय सम्पर्क में लाया जाये तो यह आवश्यक नहीं है कि उनका अंतिम ताप ही हो ।
जब दो भिन्न तापमानों की वस्तु सम्पर्क में लाई जाती हैं तब उच्च तापमान की वस्तु से ऊष्मा निम्न तापमान की वस्तु की ओर तब तक प्रवाहित होती हैं जब तक कि दोनों के तापमान समान न हो जायें । माना प्रारम्भ में गर्म वस्तु का ताप तथा ठण्डी वस्तु का ताप हैं । औसत ताप जबकि दोनों वस्तुओं की धारिताएँ समान हैं ।
Topper's Solved these Questions
- ऊष्मागतिकी का व्दितीय नियमBook:BALAJI PUBLICATIONChapter:ऊष्मागतिकी का व्दितीय नियमExercise:आँकिक प्रश्न (आत्म - निरीक्षणात्मक )
Explore 13 Videos
- ऊष्मागतिकी का व्दितीय नियमBook:BALAJI PUBLICATIONChapter:ऊष्मागतिकी का व्दितीय नियमExercise:प्रश्नावली (लघु उत्तरीय प्रश्न )
Explore 20 Videos
- ऊष्मागतिकी का व्दितीय नियमBook:BALAJI PUBLICATIONChapter:ऊष्मागतिकी का व्दितीय नियमExercise:बहुविकल्पीय प्रश्न
Explore 19 Videos
- ऊष्मा स्थानान्तरणBook:BALAJI PUBLICATIONChapter:ऊष्मा स्थानान्तरणExercise:बहुविकल्पीय प्रश्न
Explore 34 Videos
- ऊष्मागतिकी का शून्य कोटि एवं प्रथम नियम Book:BALAJI PUBLICATIONChapter:ऊष्मागतिकी का शून्य कोटि एवं प्रथम नियम Exercise:बहुविकल्पीय प्रश्न
Explore 37 Videos
Similar Questions
100∘C तथा 0∘C ताप के बीच कार्य करते उत्क्रमणीय ऊष्मा इंजन की दक्षता ज्ञात कीजिए ।
View Solutionऊष्मा इंजन क्या हैं ?
View Solutionऊष्मागतिकी का प्रथम नियम निर्दिष्ट नही करता -
View Solutionऊष्मा के स्थानान्तरण की सबसे तीव्र विधि है -
View Solutionकोन-सा कथन असत्य है
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solution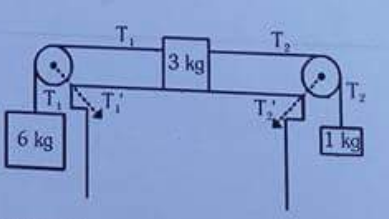
Calculate a, T1,T2,T1'&T2'.
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View Solutionभिन्न x2−5x−1(x−1)2(x−2) को आंशिक भिन्न में व्यक्त कीजिए।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View Solutionयदि किसी भिन्न का अंश, हर से 2 कम है और यदि हर में 1 जोडा जाए तो यह 12 हो जाता है तब वह भिन्न होगी ?
View Solution