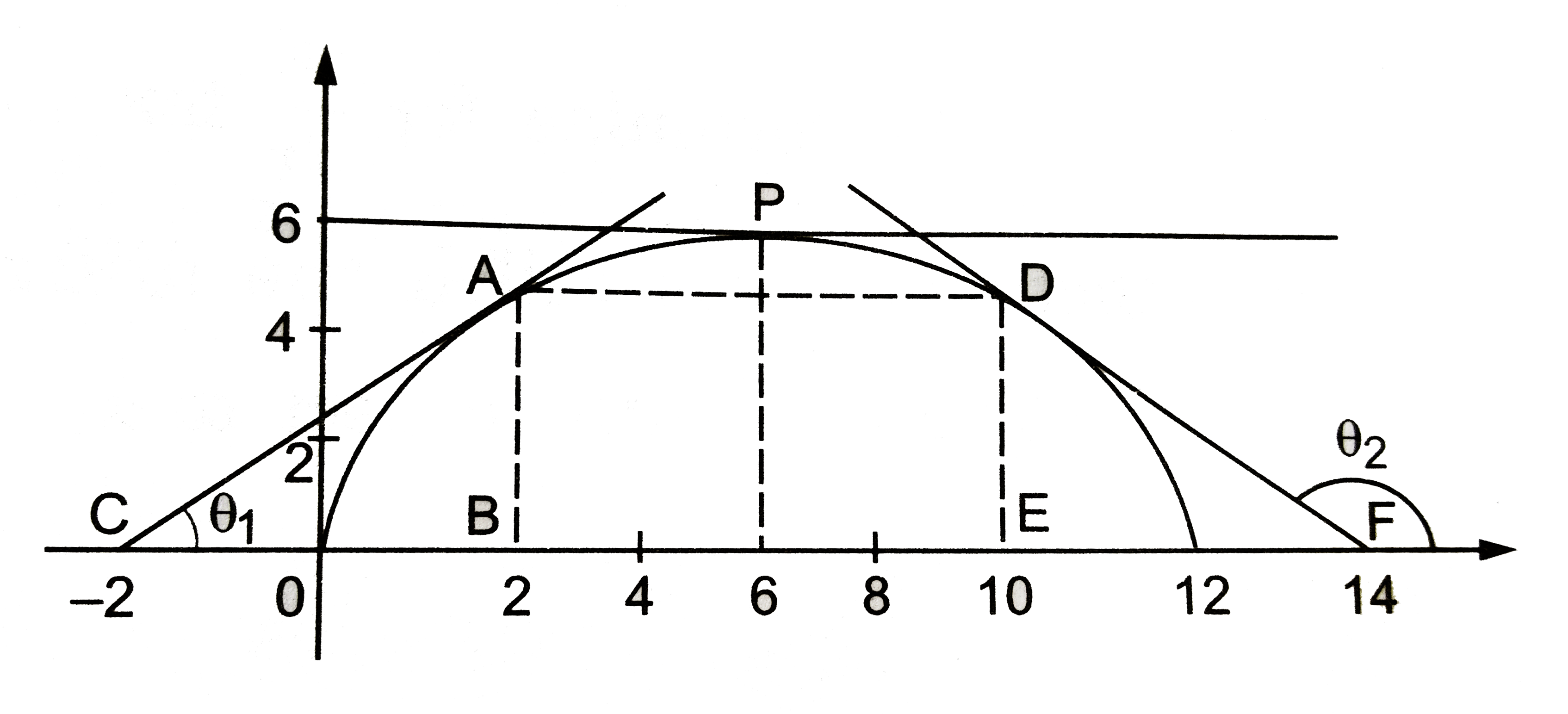
From the curve given in figure find dydxatx=2, 6 and 10.
Video Solution
Text Solution
The tangent to the curve at x=2 is AC. Its slope is tanθ1=ABBC=54
Thus, dydx=54atx=2.
The tangent to the curve at x=6 is parallel to the X-axis.
Thus, dydx=tanθ=0atx=t
The tangent to the curve at x=10 is DF. Its slope is
tanθ2=DEEF=−54 ltbr> Thus, dydx=−54atx=10
If we are given the graph of y versus x, we can find dydx at any pintof the curve bydrawing the tangent at that point and finding its slope. Evwen if the graph is not drawn and the algebraic relation bettween y and x is given in the formof an equation, we can find dydx algebraically. Let us take an example.
The area A of a square of length L is A=L2. ltbr> If we change L to L+△L, the area will change from A to A+△Aure.<br><br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C02_S01_006_S06.pngwh=80%mx-autosty≤=background:white;><br>A+/_\A=(L+/_\L)^2<br> = L^2+2L /_\L+(/_\L)^2<br>or,/_\A=2L(/_\L)+/_\L)^2<br>or,(/_\A)/ (/_\L)=2L+/_\L<br>Nowif/_\Lismadesmal≤randsmal≤r,2L+/_\Lwillappraoch2L.<br>Thus,(dA)/dL) = lim_(/_\Lrarr0)=(/_\A)/(/_\L)=2L.
|
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Worked Out Examples
Explore 18 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMAChapter:PHYSICS AND MATHEMATICSExercise:Short Answer
Explore 14 Videos
- NEWTON'S LAWS OF MOTIONBook:HC VERMAChapter:NEWTON'S LAWS OF MOTIONExercise:Exercises
Explore 42 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMAChapter:REST AND MOTION : KINEMATICSExercise:Exercises
Explore 51 Videos
Similar Questions
Knowledge Check
y=sin2x find dydx.
A−sin2xBsin2xCcos2xDNone of these
Find dydx
(x+y)2=4
View SolutionFind dydx
y=x72
View Solutiony=x6x3 , find dydx
View SolutionGiven, y=sin2x . Then find dydx .
View SolutionFind dydx, (x+y)2=x
View SolutionIf y=a2x then find dydx
View SolutionGiven dydx is directly proportional to the square of x and dydx=6 at x = 2. Then find the equation of the curve, when x = 2 and y = 4. Also find the area of the region bounded by curve between lines y = 1 and y = 3.
View Solution