A body builder exerts a force of 150 N against a bullworker and compresses it by 20 cm. Caculate the spring constant of the spring in te bullworker.
To calculate the spring constant of the spring in the bullworker, we can use Hooke's Law, which states that the force exerted by a spring is directly proportional to the displacement (compression or extension) of the spring. The formula is given by:
F=kx
Where:
- F is the force applied (in Newtons),
- k is the spring constant (in Newtons per meter),
- x is the displacement (compression or extension) of the spring (in meters).
1. Identify the Given Values:
- Force F=150N
- Compression x=20cm=0.2m (convert centimeters to meters)
2. Rearrange Hooke's Law to Solve for Spring Constant k:
k=Fx
3. Substitute the Known Values into the Equation:
k=150N0.2m
4. Perform the Calculation:
k=150÷0.2=750N/m
5. Conclusion:
The spring constant k of the spring in the bullworker is 750N/m.
- F is the force applied (in Newtons),
- k is the spring constant (in Newtons per meter),
- x is the displacement (compression or extension) of the spring (in meters).
- Force F=150N
- Compression x=20cm=0.2m (convert centimeters to meters)
k=Fx
k=150N0.2m
k=150÷0.2=750N/m
The spring constant k of the spring in the bullworker is 750N/m.
Topper's Solved these Questions
- THE FORCESBOOK - HC VERMACHAPTER - THE FORCESEXERCISE - Objective -2
2 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises
35 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
Similar Questions
On compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.
View SolutionA mass of 2 kg is suspended from a vertical spring. An additional force of 2.5 N stretches it by 1 cm. (i) Calculate the force constant. (ii) Calculate the frequecny of oscillations, if the spring is stretched by the given force and then released.
View Solution
Knowledge Check
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/mA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
A0.5JB2.5JC5JD10 J
A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. The spring constant of the spring is 6mv2nx2. Find value of n.
View SolutionFigure shows a force compression curve of a spring. A body of mass 5kg moving with the velocity of 8m/s hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
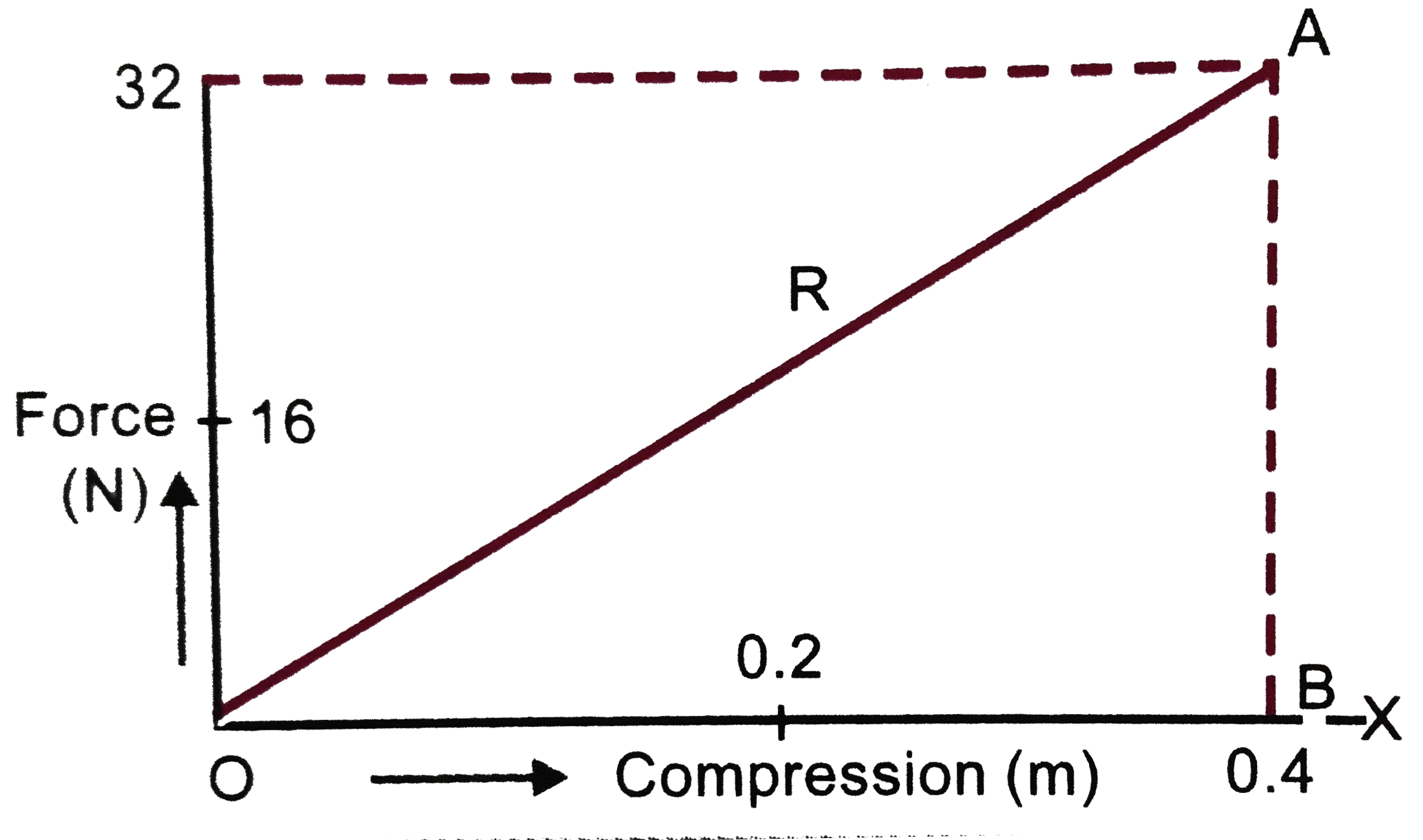
View SolutionA spring compressed by 0.1m develips a restoring force 10N. A body of mass 4kg is placed on it. Deduce (i) the force constant of the spring (ii) the depression of the spring under the weight of the body ( take g=10N/kg) and (iii) the period of oscillation, if the body is left free.
View SolutionYou push a 2.0 kg block against a horizontal spring , compressing the spring by 12 cm. Then You release the block, and the spring sends it sliding across a tabletop. It stops 75 cm from where you released it. The spring constant is 170 N/m. What is the block-table coefficient of kinetic friction ?
View SolutionA spring compressed by 0.2 m develops a restoring force of 25 N. A body of mass 5 kg is placed over it. Deduce (i) force constant of the spring (ii) the depression of the spring under the weight of the body and (iii) the period of oscillation, if the body is disturbed. Take g=10Nkg−1.
View Solution