A body of weight w1 is suspended from the ceiling of a room through as chain of weight w2. The ceiling pulls the chain by a force
w1
w2
w1+w2
w1+w22
The correct Answer is:C
To solve the problem, we need to determine the force that the ceiling exerts on the chain when a body of weight w1 is suspended from it through a chain of weight w2.
1. Identify the System:
We have a body of weight w1 suspended from a chain that has a weight w2. The entire system can be treated as a single unit where both the body and the chain contribute to the total weight that the ceiling must support.
Hint: Consider the entire system as a single entity to simplify calculations.
2. Calculate the Total Weight:
The total weight that the ceiling has to support is the sum of the weight of the body and the weight of the chain. Therefore, the total weight W is given by:
W=w1+w2
Hint: Remember that the ceiling must support both the body and the chain together.
3. Force Exerted by the Ceiling:
The force that the ceiling exerts on the chain must equal the total weight of the system (the body plus the chain). According to Newton's second law, the upward force exerted by the ceiling (let's denote it as F) must balance the downward gravitational force (the total weight). Thus, we have:
F=w1+w2
Hint: The force exerted by the ceiling is equal to the total weight acting downwards.
4. Conclusion:
Therefore, the force that the ceiling pulls the chain with is w1+w2.
Final Answer: The ceiling pulls the chain with a force of w1+w2.
We have a body of weight w1 suspended from a chain that has a weight w2. The entire system can be treated as a single unit where both the body and the chain contribute to the total weight that the ceiling must support.
The total weight that the ceiling has to support is the sum of the weight of the body and the weight of the chain. Therefore, the total weight W is given by:
W=w1+w2
The force that the ceiling exerts on the chain must equal the total weight of the system (the body plus the chain). According to Newton's second law, the upward force exerted by the ceiling (let's denote it as F) must balance the downward gravitational force (the total weight). Thus, we have:
F=w1+w2
Therefore, the force that the ceiling pulls the chain with is w1+w2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 2
9 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
One end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionA wire is suspended from the ceiling and stretched under the action of weight F suspended from its other end. The force exerted by the ceiling on it is equal and opposite to the weight.
View Solution
Knowledge Check
A heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
AΔL=ϕgL2YBΔL=2ϕgL2YCΔL=ϕgL22YDΔL=ϕgLYOne end of a wire of length L and weight w is attached rigidly to a point in roof and a weight w1 is suspended from its lower end. If A is the area of cross-section of the wire then the stress in the wire at a height 3L4 from its lower end is
Aw1ABw1+w4ACw1+3w4ADw1+w2AOne end of a uniform wire of length L and weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
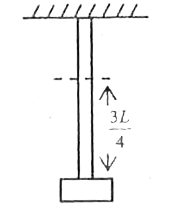 AW1SB[W1+(W/4)]SC[W1+(3W/4)]SDW1+WS
AW1SB[W1+(W/4)]SC[W1+(3W/4)]SDW1+WS
One end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionA weight is suspended from the ceiling of a lift by a spring balance. When the lift is stationary the spring balance reads W . If the lift suddenly falls freely under gravity, the reading on the spring balance will be
View SolutionA metre scale is supported on a wedge at its centre of gravity. A body of weight w is suspended from the 15 cm mark and another weight of 30 gram suspended from 71 cm mark balances it the metre scale remains perfectly horizontal. What is the weight of the body? Neglect the weight of the centre scale.
View SolutionA string of length L and radius r elongated by x due to its own weight, when suspended from the ceiling from its one end. If another string of same material, same length and radius double the initial is suspended from its one end then elongation due to its own weight will be
View Solution
