The two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by gravity during the fourth second after the system is released from rest.
To solve the problem of finding the work done by gravity during the fourth second after the system is released from rest in an Atwood machine with masses 2.0 kg and 3.0 kg, we can follow these steps:
Step 1: Identify the masses and the gravitational force
We have two masses:
- m1=2.0kg (the lighter mass)
- m2=3.0kg (the heavier mass)
The gravitational force acting on each mass is given by:
- For m1: Fg1=m1⋅g=2.0kg⋅10m/s2=20N
- For m2: Fg2=m2⋅g=3.0kg⋅10m/s2=30N
Step 2: Determine the acceleration of the system
Using Newton's second law, we can set up the equations for both masses.
For the 3 kg mass (going down):
m2g−T=m2a⇒30−T=3a(1)
For the 2 kg mass (going up):
T−m1g=m1a⇒T−20=2a(2)
Adding equations (1) and (2):
30−20=3a+2a⇒10=5a⇒a=2m/s2
Step 3: Calculate the distance traveled during the fourth second
The distance traveled by the masses during the nth second can be calculated using the formula:
sn=u+a2(2n−1)
Since the system starts from rest, u=0:
s4=0+22(2⋅4−1)=1⋅(8−1)=7m
Step 4: Calculate the work done by gravity
The work done by gravity on each mass can be calculated as follows:
For the 3 kg mass (going down):
Wg2=m2⋅g⋅h=3⋅10⋅7=210J
For the 2 kg mass (going up):
Wg1=−(m1⋅g⋅h)=−(2⋅10⋅7)=−140J
Step 5: Calculate the net work done by gravity
The net work done by gravity on the system during the fourth second is:
Wnet=Wg2+Wg1=210J−140J=70J
Final Answer
The work done by gravity during the fourth second after the system is released from rest is 70 Joules.
---
We have two masses:
- m1=2.0kg (the lighter mass)
- m2=3.0kg (the heavier mass)
- For m1: Fg1=m1⋅g=2.0kg⋅10m/s2=20N
- For m2: Fg2=m2⋅g=3.0kg⋅10m/s2=30N
Using Newton's second law, we can set up the equations for both masses.
m2g−T=m2a⇒30−T=3a(1)
T−m1g=m1a⇒T−20=2a(2)
30−20=3a+2a⇒10=5a⇒a=2m/s2
The distance traveled by the masses during the nth second can be calculated using the formula:
sn=u+a2(2n−1)
Since the system starts from rest, u=0:
s4=0+22(2⋅4−1)=1⋅(8−1)=7m
The work done by gravity on each mass can be calculated as follows:
Wg2=m2⋅g⋅h=3⋅10⋅7=210J
Wg1=−(m1⋅g⋅h)=−(2⋅10⋅7)=−140J
The net work done by gravity on the system during the fourth second is:
Wnet=Wg2+Wg1=210J−140J=70J
The work done by gravity during the fourth second after the system is released from rest is 70 Joules.
Topper's Solved these Questions
Similar Questions
The heavier bock in an atwood machine has a mass twice that of the lighter one. The tension in the stirng is 16.0 N when the sytem is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is releaed from rest.
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is refosed from rest ,
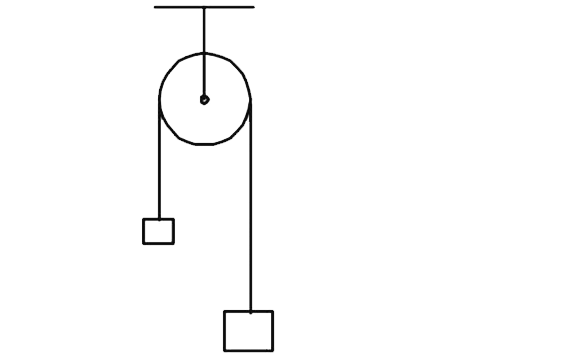
View Solution
Knowledge Check
A light in extensible string that goes over a smooth fixed pulley as shown in the figure connect two blocks of masses 0.36kgand0.72kg. Taking g=10m/s2. Find the work done by string on the block of mass 0.36kg during the first second after the system is released from rest.
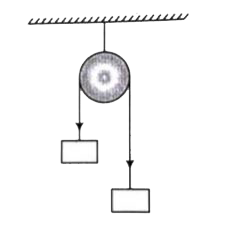 A4JB2JC8JD10J
A4JB2JC8JD10JA particle of mass 2 kg travels according to S=3t3+2t Find the work done in 3 second of time
A6889 JB6885 JC1782 JDNone of these
The acceleration of 3 kg block in the arrangement shown in the diagram ,when the given system is released from rest is
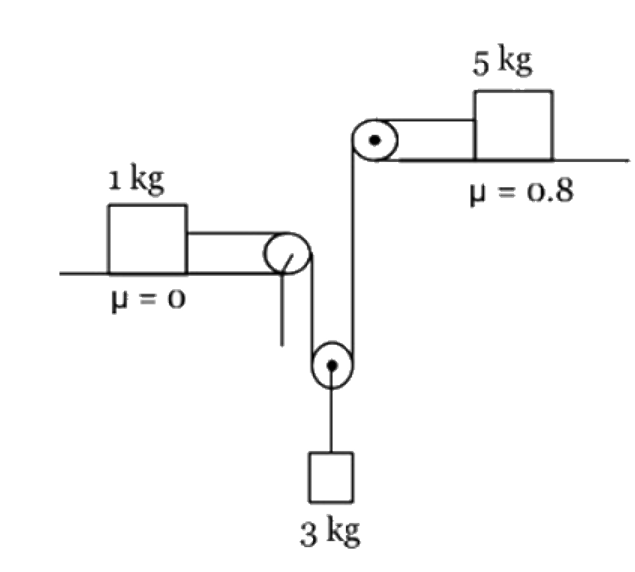
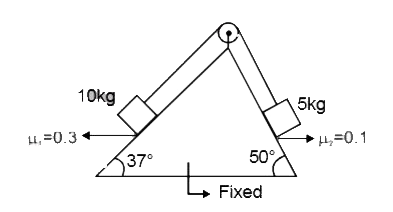
View SolutionTwo blocks of masses 5kg and 10kg are attached with the help of light string and placed on a rough incline as shown in the figure. Coefficients of friction are as marked in the figure. The system is released from rest. Determine the acceleration of the two blocks.
View SolutionA spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
View SolutionA spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionTwo unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.

View Solution
