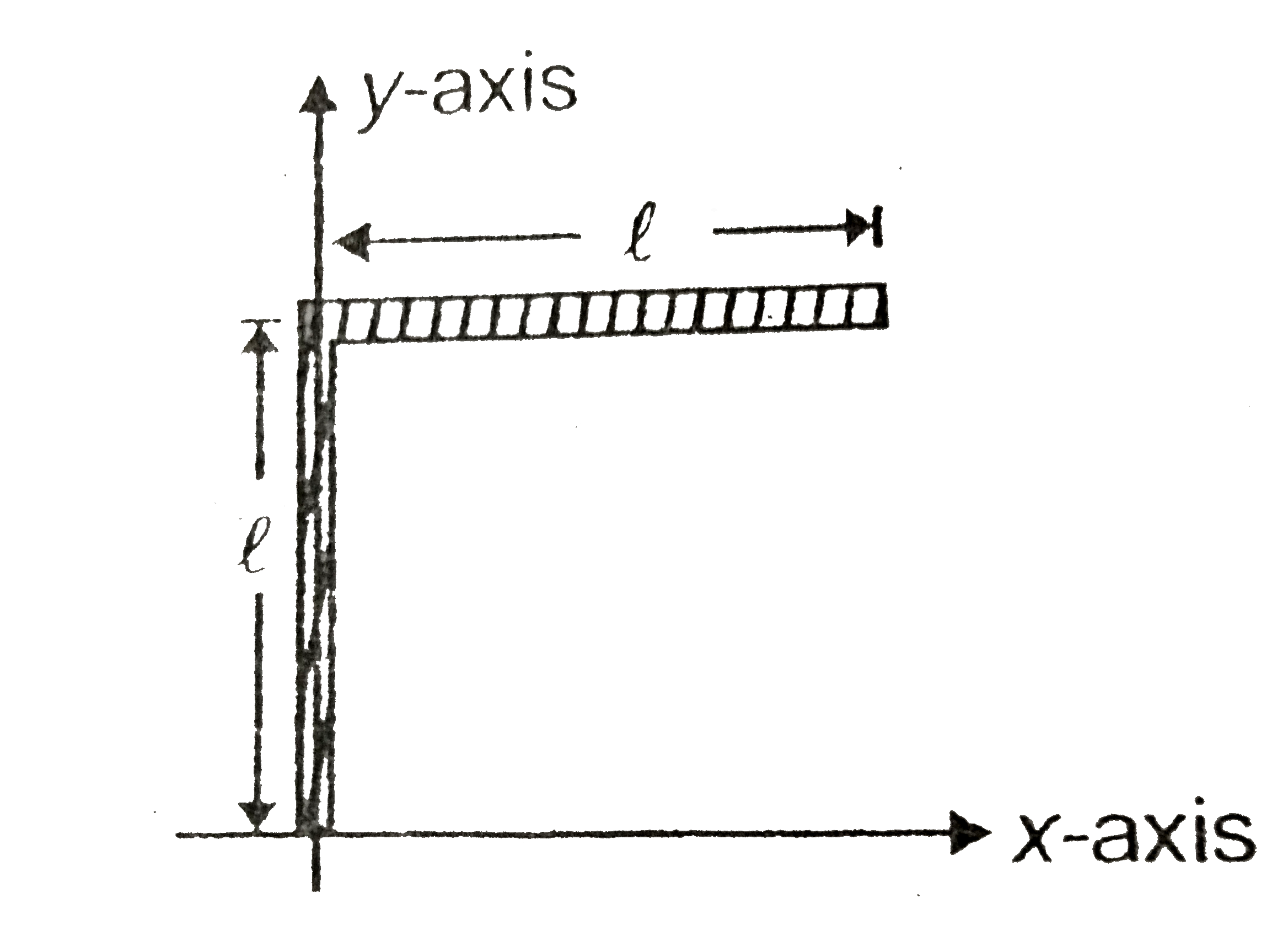Seven homogeneous bricks, each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L10. Find the x-coordinate of the centre of mass relative to the origin shown.

Let 0(0,0)betheorignofthesystem.EachbrickisofmassMand≤n>hL,Eachbrickisdisplacedw.r.to≠∈contactbyL/10.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_057_S01.pngwh=80%mx-autosty≤=background:white;><br>:. The X coordiN/Ate of the centre of mas Xcm
=1/{7mL/10)^((mL)/2+m(L/2+L/10)+.......+m(L/2)}/(7mL10)
Xcm=L2+L2+L10+L5+L2+3L10+L2+L5+L2+L10+L27
=7L2+5L10+2L57=22L35
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
Knowledge Check
Find the x coordinate of the centre of mass of the bricks shown in figure :
 A2425lB2524lC1516lD1615
A2425lB2524lC1516lD1615From a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
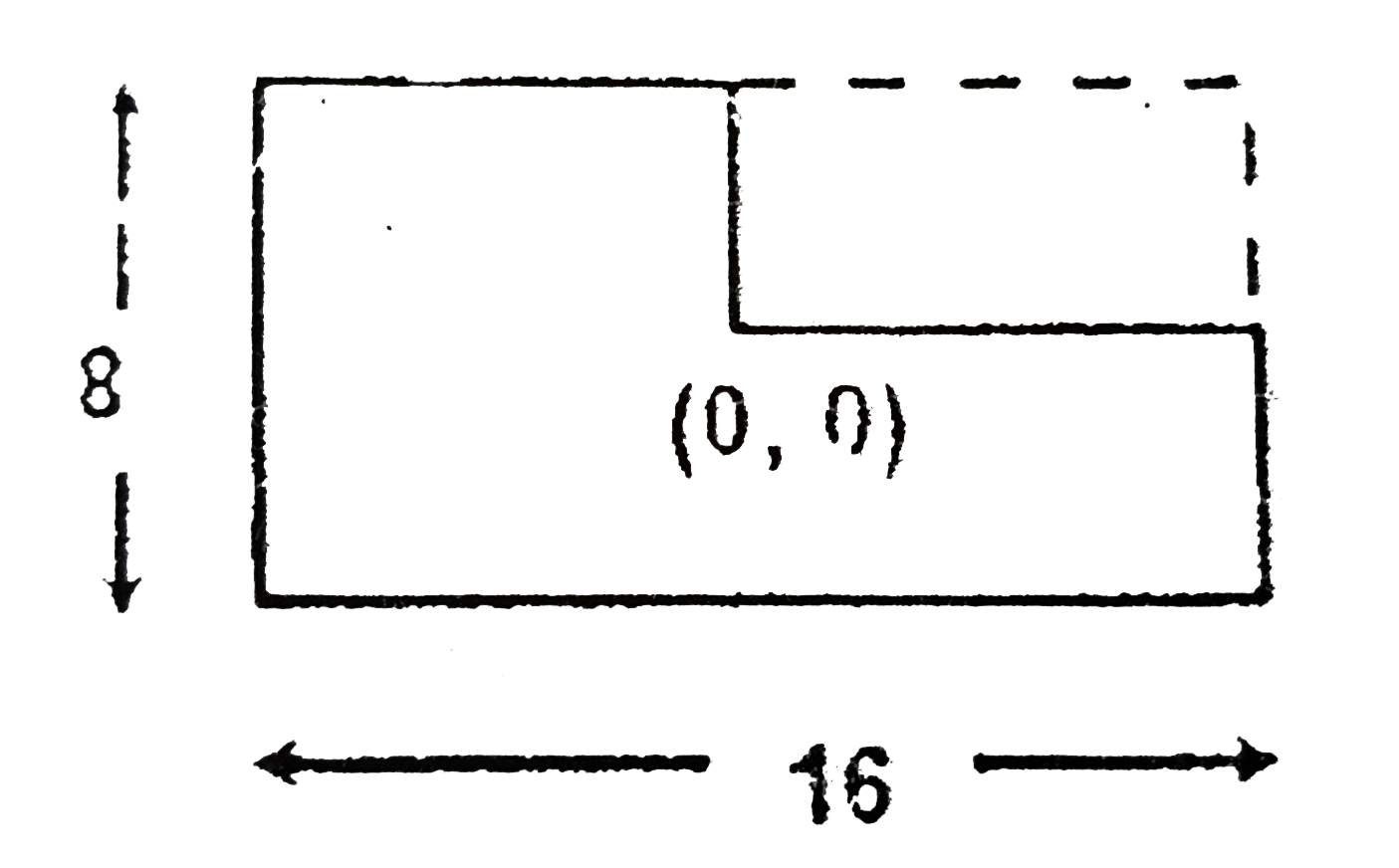 A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)
A(4/3,2/3)B(0,2/3)C(4/3,0)D(−4/3,−2/3)Five uniform circular plates, each of diameter b and mass m are laid out in a pattern shown. Using the origin shown, find the y co-ordinate of the centre of mass of the five-plate system.
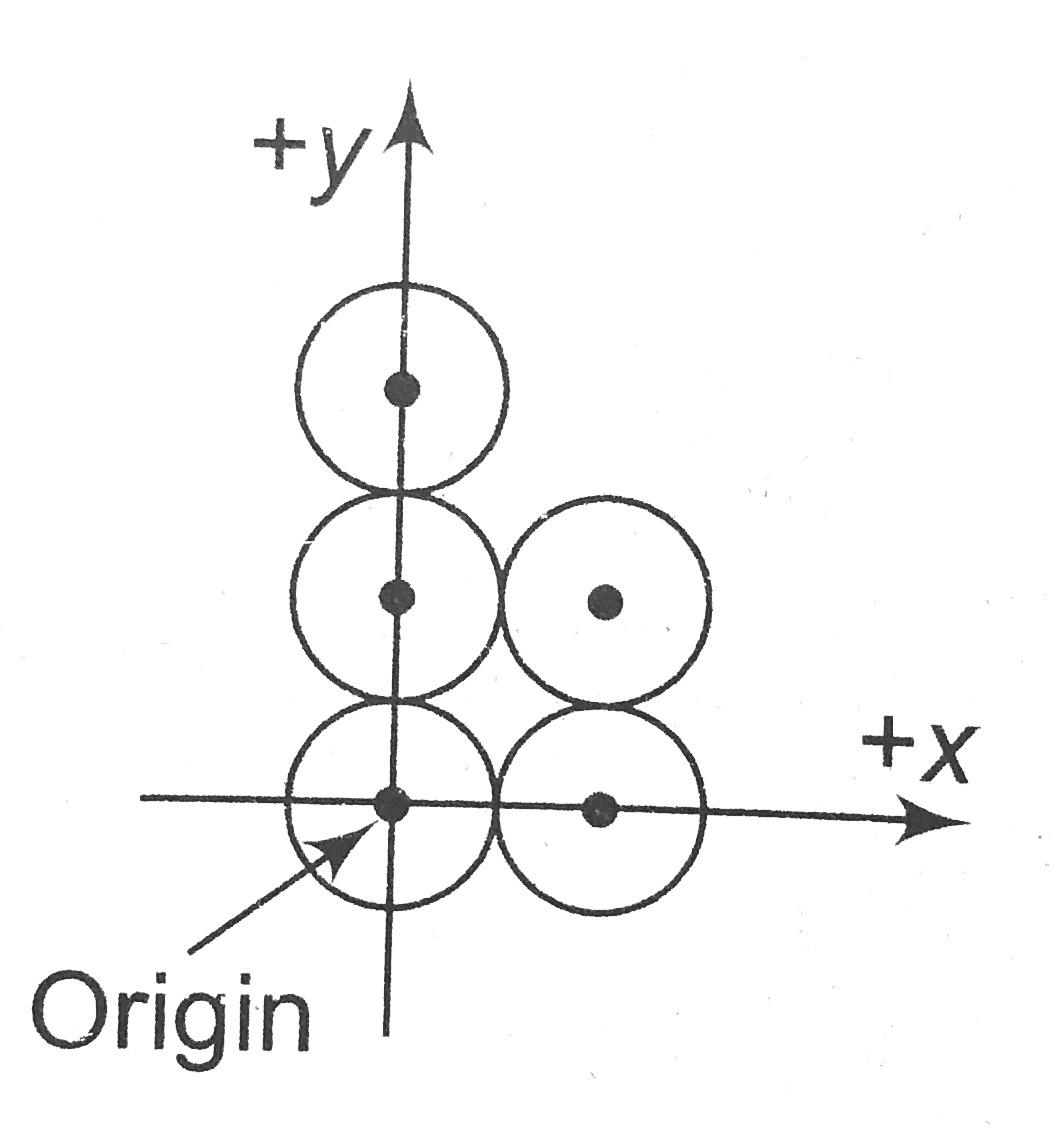 .Ab/5Bb/3C4b/5D2b/5
.Ab/5Bb/3C4b/5D2b/5
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionSix rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
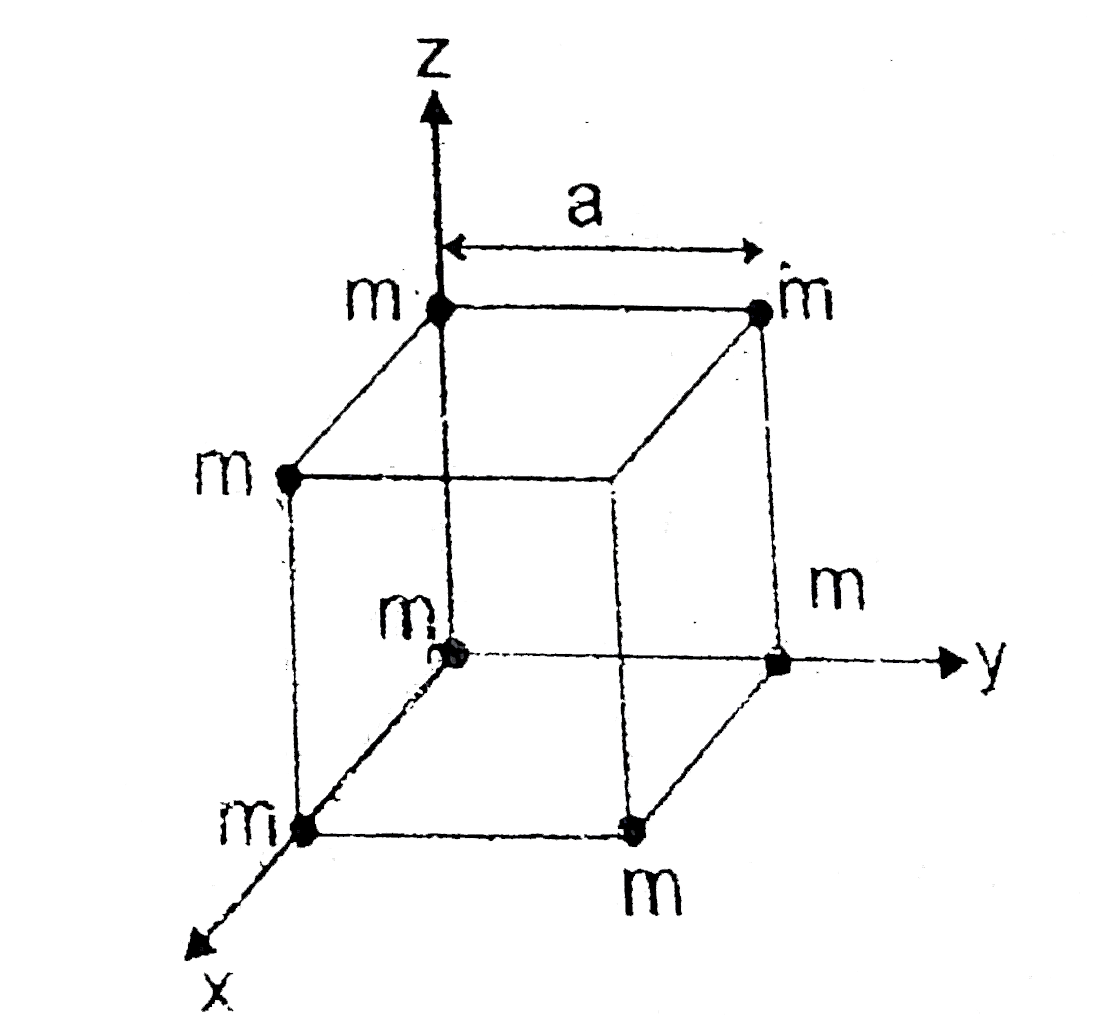
View SolutionSeven particles, each of mass m are placed at the seven corners of a cube of side 'a', but one corner is vacant, as shown in figure. If the x−coordinates of the centre of mass of the system is nam. Where n and m are least integer values. Then find vlaue of m−n.
View SolutionFind the position of centre of mass of the uniform planner sheet shown in figure with respect to the origin (O) -
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View Solution