Find the moment of inertia of a pair of spheres, each having a mass m and radius r kept in contact about the tangent passing through the point of contact.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

The two bodies of mass m and radius are movgn along the common tangent. Therefore moment of inertial of th first body about XY tangent
$m r^{2} + \frac{2}{5} m r^{2}$
$= m o m e n t o f \in e r t i a o f t h e s e n c o n b o d y X Y tan \geq n t < b r >$ =mr^2+2/5mr^2=7/5mr^2 $< b r > T h e r e f or e, \neq t m o m e n t o f \in e r t i a < b r >$ =7/5mr^2+7/5mr^2

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

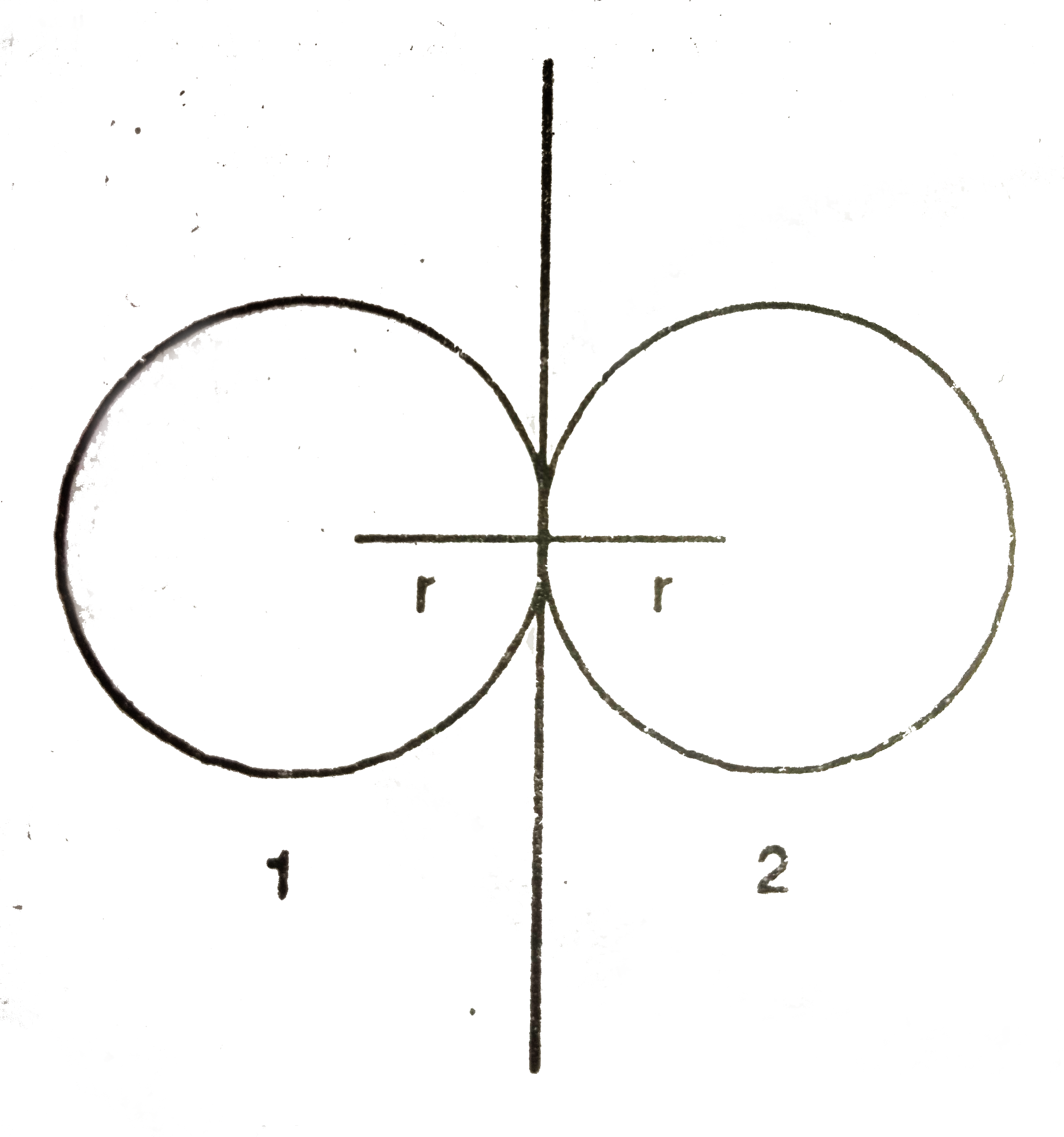
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A $\frac{2}{5} M R^{2}$
B $\frac{6}{3} M R^{2}$
C $\frac{4}{5} M R^{2}$
D $\frac{7}{5} M R^{2}$
Question 2 - Select One
The moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
A $\frac{1}{2} M r^{2}$
B $M t^{2}$
C $\frac{2}{5} M r^{2}$
D $\frac{1}{4} M r^{2}$

HC VERMA-ROTATIONAL MECHANICS-Exercises

Home
Ask Doubt
Profile