The resultant force acting on a particle executing simple harmonic motion is 4N when it is 5cm away from the centre of oscillation. Find the spring constant.
To find the spring constant k for a particle executing simple harmonic motion (SHM) given the resultant force and the displacement from the center of oscillation, we can follow these steps:
Step 1: Understand the relationship between force and displacement in SHM
In simple harmonic motion, the force F acting on the particle is given by Hooke's Law:
F=−k⋅x
where:
- F is the restoring force (in Newtons),
- k is the spring constant (in Newtons per meter),
- x is the displacement from the equilibrium position (in meters).
Step 2: Identify the given values
From the problem, we know:
- The resultant force F=4N (magnitude),
- The displacement x=5cm=0.05m.
Step 3: Substitute the values into the equation
Using the magnitude of the force in the equation:
4=k⋅0.05
Step 4: Solve for the spring constant k
Rearranging the equation to solve for k:
k=40.05
Calculating this gives:
k=40.05=80N/m
Final Answer
The spring constant k is 80N/m.
---
In simple harmonic motion, the force F acting on the particle is given by Hooke's Law:
F=−k⋅x
where:
- F is the restoring force (in Newtons),
- k is the spring constant (in Newtons per meter),
- x is the displacement from the equilibrium position (in meters).
From the problem, we know:
- The resultant force F=4N (magnitude),
- The displacement x=5cm=0.05m.
Using the magnitude of the force in the equation:
4=k⋅0.05
Rearranging the equation to solve for k:
k=40.05
Calculating this gives:
k=40.05=80N/m
The spring constant k is 80N/m.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
The acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
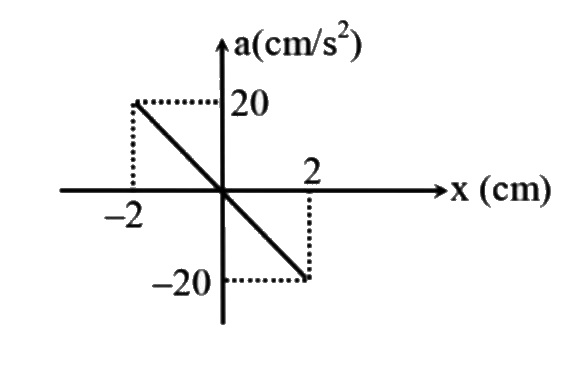
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View Solution
Knowledge Check
The phase of a particle executing simple harmonic motion is π2 when it has
AMaximum velocityBMaximum accelerationCMaximum energyDMaximum displacementThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
A(a) 0.01sB(b) 10sC(c ) 0.1sD(d) 100s
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle isA4s−1B(52π)s−1C(18π)s−1D(12π)s−1
The velocity of a particle executing a simple harmonic motion is 13ms−1 when its distance from the equilibrium position (Q) is 3 m and its velocity is 12 ms−1 when it is 5 m away from Q. The frequency of the simple harmonic motion is
View SolutionWhen the potential energy of a particle executing simple harmonic motion is one-fourth of its maximum value during the oscillation, the displacement of the particle from the equilibrium position in terms of its amplitude a is
View SolutionWhen the potential energy of a particle executing simple harmonic motion is one-fourth of its maximum value during the oscillation, the displacement of the particle from the equilibrium position in terms of its amplitude a is:
View SolutionThe total mechanical energy of a particle executing simple harmonic motion is E when the displacement is half the amplitude of its kinetic energy will be
View SolutionThe potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
View Solution
