Describe the motion of the mass m shown in figure. The walls and the block are elastic.
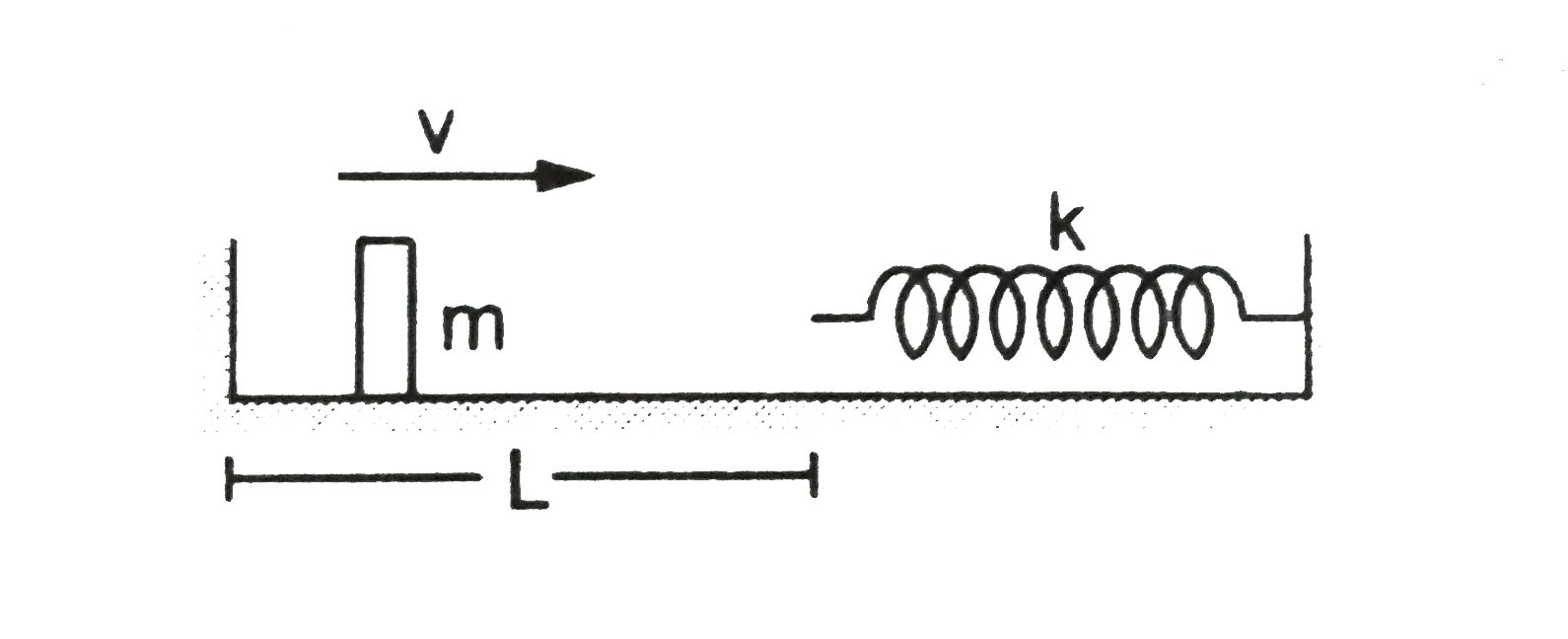
The block reaches the sring with a speed v. It now compresses te spring . The block is decelerated due toteh sprng force comes to rest when 12mv2=12kx2 and returns back. It is accelerated due toteh spring force till the spring acquires its N/Atural length. The contact of the block with the spring is now broken. At this instant it has regained its speed v (towards left) as teh sprig is unstretched and no potential energy is stored. This proces takes half the period of oscillation, i.e. π√mk. The block strikes the left wall after a time Lv and as the collision is elstic it rebounds with the same speed v. After a time Lv, it again reaches the spring and the process is repeated. The block thus undergoes periodic motion with time period π√mk+2Lv
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
A block of mass m is at rest on the another blcok of same mass as shown in figure. Lower block is attached to the spring then the maximum amplitude of motion so that both the blcok will remain in contact is
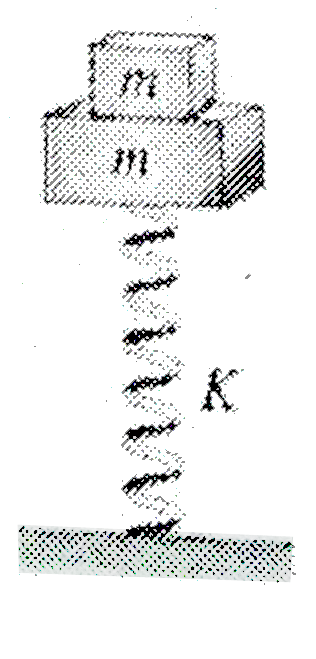 Amg2kBmgkC2mgkD3mg2k
Amg2kBmgkC2mgkD3mg2kTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :
 AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
A block of mass 0.9kg attached to a spring of force constant k is lying on a frictionless floor. The spring is compressed to √2cm and the block is at a distance 1/√2cm from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is 0.2sec. Find the approximate value of k

View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View SolutionA block mass 'm' is kept on the ground as shown in figure.
Are forces acting on block action - reaction pair.
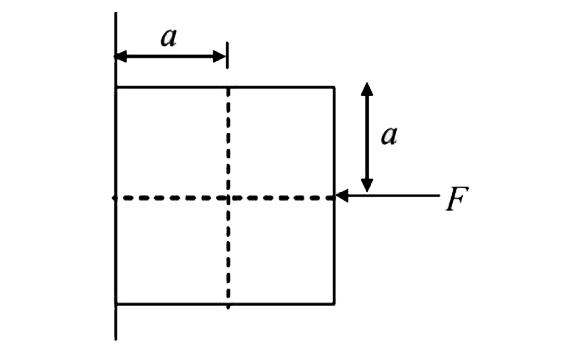
View SolutionA block of mass m is at rest under the action of force F against a wall as shown in figure. Which of the following statement is incorrect?
View Solution