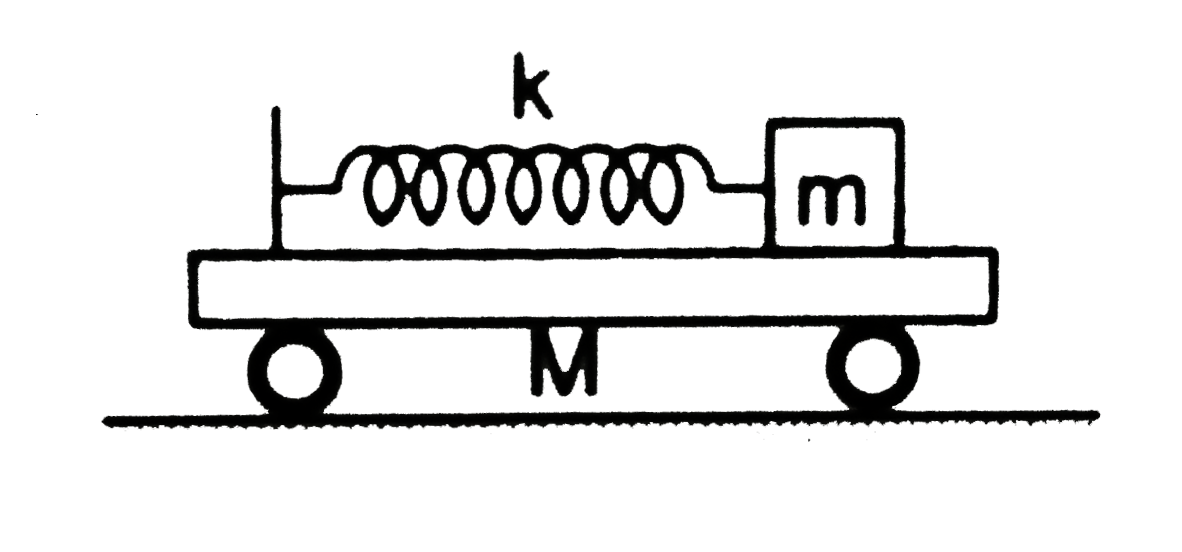
All the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
The correct Answer is:A, B
Let the amplitude of oscillation of m and M be x1andx2 respectively.
a. From law of conservation of momentum mx1=Mx2 ………1
[Block and mass oscillates in opposite direction bt xp→ stretched part]. From equation 1 and equation 2<br>:. x_0=x_1+m/Mx_1<br>=((M+m)/M)x<br>so, x_2=x_0-x_1<br>x_0[1-M/(M+m)]<br>=(mx_0)/(M+m)respectively<br>b.Atanyposition,≤tthevelocitybev_1 and v_2respectively.Herev_1 velocity of m'withrespect→M.Bye≠rgymethod,<br>TotalE≠rgy=Constant<br>1/2mv_2^2+1/2m(v_1-v_2)^2+1/2k(x_1+x_2)^2<br>>=constant.......3<br>[v_1-v-2=|o|lutevelocityofmassmasseenomtheroad]<br>Mx_2=mx_1<br>rarr x_1=(M/m)x_2.........4<br>Mv_2=m(v_1-v_2)<br>rarr (v_1-v_2)=(M/m)v_2..........5<br>Pu∈gtheabovevalues∈equation3we≥t<br>1/2Mv_2^I2+1/2m M/m^2 v_2^2+1/2kx_2^2(1+M/m)<br>:.M(1+M/m)v_2^2+k(1+M/m)x_2^2=constant<br>rarr Mv_2^2+k(1+M/m)x_2^2=constant<br>Tak∈gderivativeof⊥hss,<br>M_2v_2(dv_2)/(dt)=k((M+m)/m)2x_2(dx_2)/(dt)=0<br>rarr ma_2+k((M+m)/m)x_2=0<br>[because v_2=(dx_2)/(dt)]<br>a_2/x_2=(-kM+m)/(Mm)omega^2<br>:. omega=(-k(M+m))/(Mm)<br>Sotimeperiod<br>T=2pi sqrt((Mm)/(M+m))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Two masses m1andm2 re connected by a spring of spring constant k and are placed on as frictionless horizontal surface. Initially the spring is stretched through a distance x0 when the system is released from rest. Find the distance moved by the two masses before they again come to rest.
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
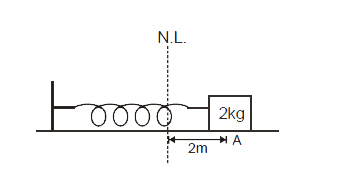
View Solution
Knowledge Check
In the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
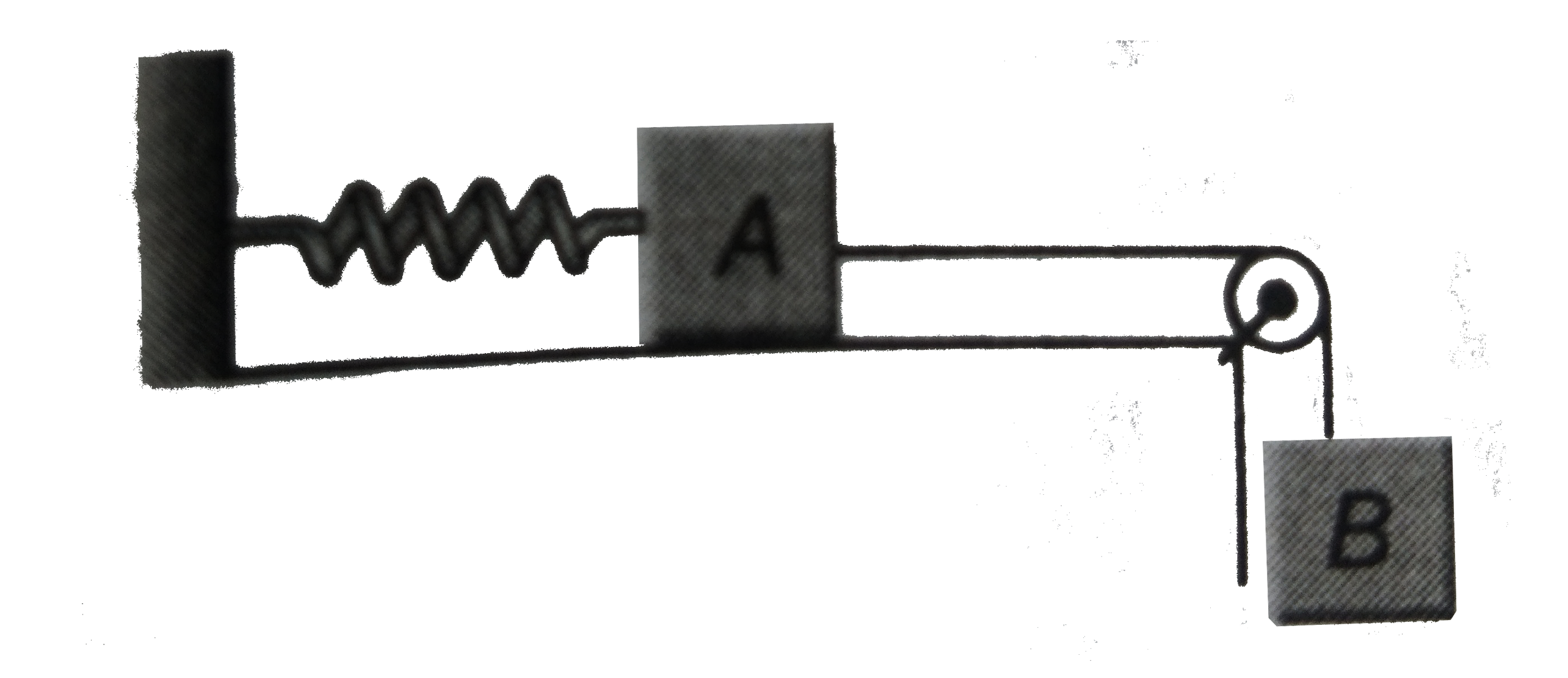 .AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
.AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
In the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
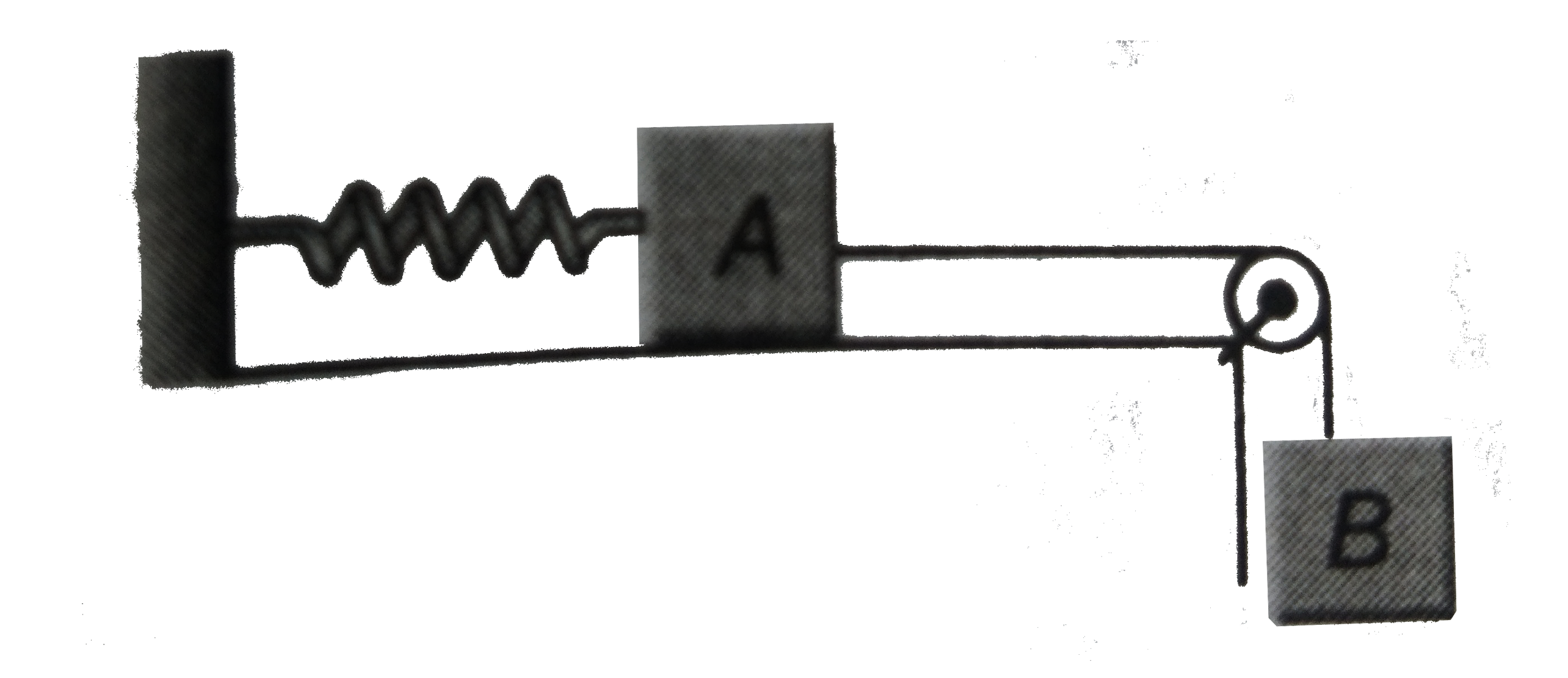 .
.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
