One end of a nylon rope of length 4.5 m and diameter 6 mmis fixed to a tree limb. A monkey weighing 100 N jumps to catch the free end and stays there. Find the elongation of the rope and the corresponding change in the diameter. Young modulus of nylon =0.2.
To solve the problem of finding the elongation of the nylon rope and the corresponding change in its diameter when a monkey weighing 100 N jumps and catches the free end, we will follow these steps:
Step 1: Calculate the Cross-Sectional Area of the Rope
The diameter of the rope is given as 6 mm. First, we need to convert this to meters:
Diameter=6 mm=0.006 m
The radius r is half of the diameter:
r=0.0062=0.003 m
The cross-sectional area A of the rope can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.003)2≈2.827×10−5 m2
Step 2: Calculate the Stress on the Rope
Stress σ is defined as force per unit area:
σ=FA
Where F is the weight of the monkey (100 N):
σ=1002.827×10−5≈3.53×106 N/m2
Step 3: Calculate the Strain in the Rope
Young's modulus Y is defined as the ratio of stress to strain:
Y=σϵ
Where ϵ is the strain. Rearranging gives:
ϵ=σY
Substituting the values of σ and Y (given as 0.2 × 10^9 N/m²):
ϵ=3.53×1060.2×109=0.01765
Step 4: Calculate the Elongation of the Rope
The elongation ΔL can be calculated using the formula:
ΔL=ϵ×L
Where L is the original length of the rope (4.5 m):
ΔL=0.01765×4.5≈0.0794 m=79.4 mm
Step 5: Calculate the Change in Diameter
Using Poisson's ratio ν (given as 0.02), the change in diameter Δd can be found using the relationship:
Δd=−ν×ϵ×d
Where d is the original diameter (0.006 m):
Δd=−0.02×0.01765×0.006≈−0.00000235 m=−2.35 mm
Summary of Results
- Elongation of the rope ΔL≈79.4 mm
- Change in diameter Δd≈−0.00235 m or −2.35 mm
---
The diameter of the rope is given as 6 mm. First, we need to convert this to meters:
Diameter=6 mm=0.006 m
The radius r is half of the diameter:
r=0.0062=0.003 m
The cross-sectional area A of the rope can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.003)2≈2.827×10−5 m2
Stress σ is defined as force per unit area:
σ=FA
Where F is the weight of the monkey (100 N):
σ=1002.827×10−5≈3.53×106 N/m2
Young's modulus Y is defined as the ratio of stress to strain:
Y=σϵ
Where ϵ is the strain. Rearranging gives:
ϵ=σY
Substituting the values of σ and Y (given as 0.2 × 10^9 N/m²):
ϵ=3.53×1060.2×109=0.01765
The elongation ΔL can be calculated using the formula:
ΔL=ϵ×L
Where L is the original length of the rope (4.5 m):
ΔL=0.01765×4.5≈0.0794 m=79.4 mm
Using Poisson's ratio ν (given as 0.02), the change in diameter Δd can be found using the relationship:
Δd=−ν×ϵ×d
Where d is the original diameter (0.006 m):
Δd=−0.02×0.01765×0.006≈−0.00000235 m=−2.35 mm
- Elongation of the rope ΔL≈79.4 mm
- Change in diameter Δd≈−0.00235 m or −2.35 mm
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
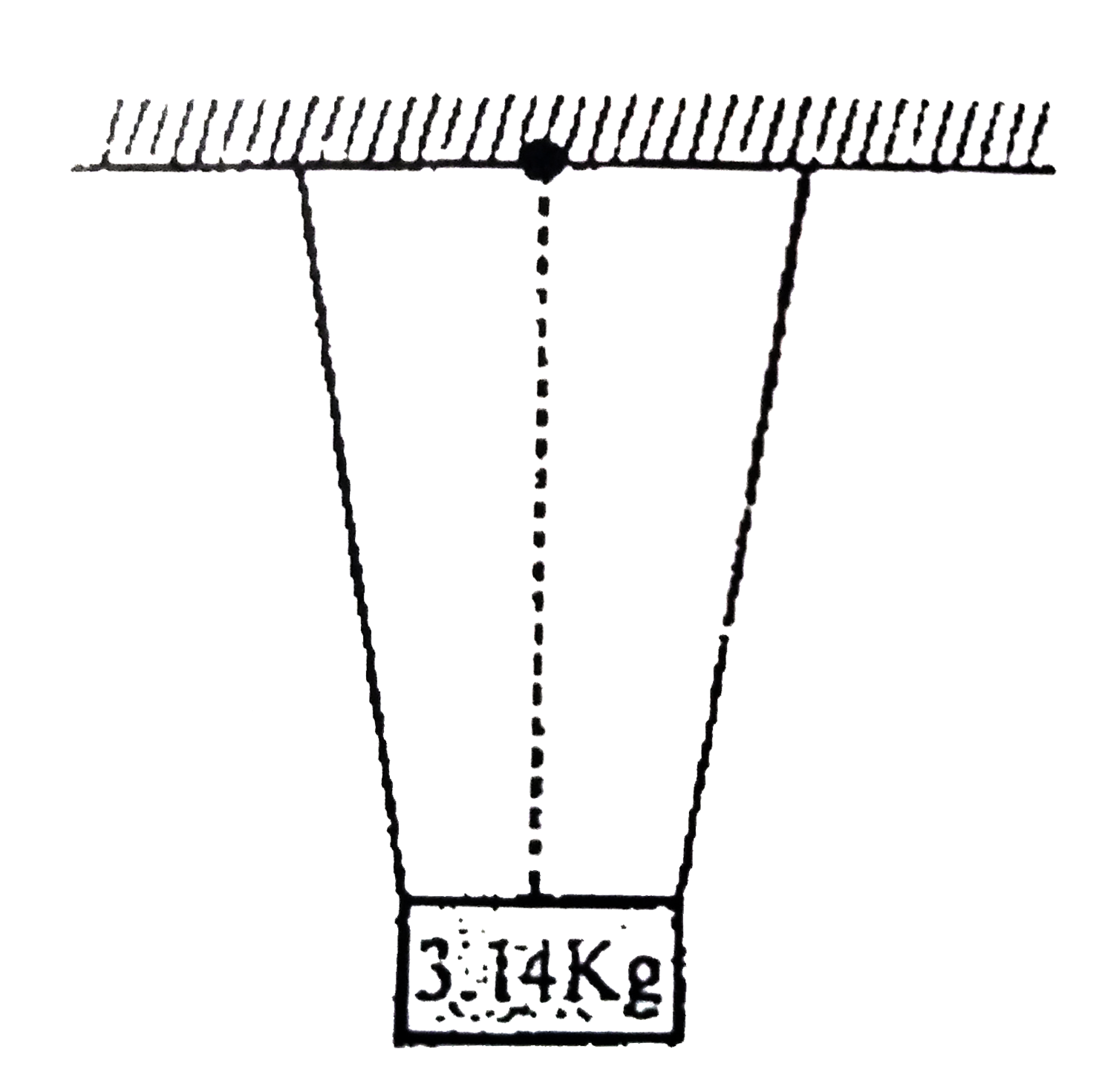
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View Solution
Knowledge Check
One end of a wire 2 m long and dameter 2 mm is fixed in a celling . A naughty boy of mass 10 kg jumps to catch the free end and stays, there. The chamge is length of wire is (Taker=10m/s2,Y=2×1011N/m2)
A3.185×10−5B2 mmC3 mmD4mmA uniform steel wire of length 3.14 m and diameter 2×10−3 m is fixed at its upper end. When a mass of 10 kg is attached to its lower end, the extension of the wire is 1×10−3 m. The Young's modulus of elasticity is,
A9.8×108N/m2B9.8×109N/m2C9.8×1010N/m2D9.8×1011N/m2If one end of a diameter of the circle x2+y2−4x−6y+11=0 is (3,4), then find the coordinates of the other end of the diameter.
A(2,1)B(1,2)C(1,1)DNone of these
A steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View SolutionA horse is tied to a rope of length 5 m and the order end of the rope is tied to a pole, find the displacement and the distance travelled by the horuse in the following cases.
i. When the horse makes half revolution along a circular path.
ii. when it markes one full revolution.
iii. when it makes 34 th of the revolution.
View SolutionA rod of length 6m has specific gravity ρ(=25/36). One end of the rod is tied to a 5m long rope, which in turn is tied to the floor of a pool 10m deep, as shown. Find the length (in m) of the part of rod which is out of water.

View SolutionA rope of length of 2m is tied between two ends . If the speed of transverse waves propagating in the rope is 4ms−1 and the tension in the rope is 2 N , find the mass of the rope is C.G.S units .
View SolutionThe Young's modulus of a rope of 10 m length and having diameter of 2 cm is 20×1011 dyne cm−2 . If the elongation produced in the rope is 1 cm, the force applied on the rope is
View Solution
