A light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25dy≠cm−1.Takeg=10ms−2
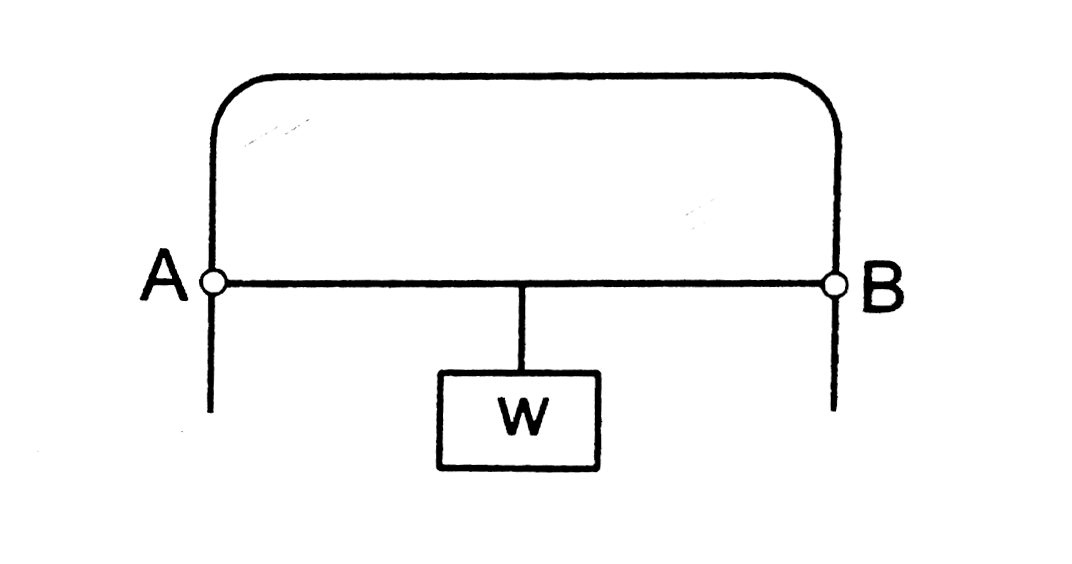
Soap solutioin film will be formed on both sides of the frame. Each film is in contact with the wire along a distanc eo 10 cm The force exerted by the film on the wire
=2×(10cm)×(25dy≠cm−1)
=500dy≠=5×10−3N.
This force acts vertically upward and should be balanced by the load. Hence the load that should be suspended is 5×10−3N. The mass of the load should be
5×106−3N10ms−2=5×10−4kg=0.54g.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Short Answer
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
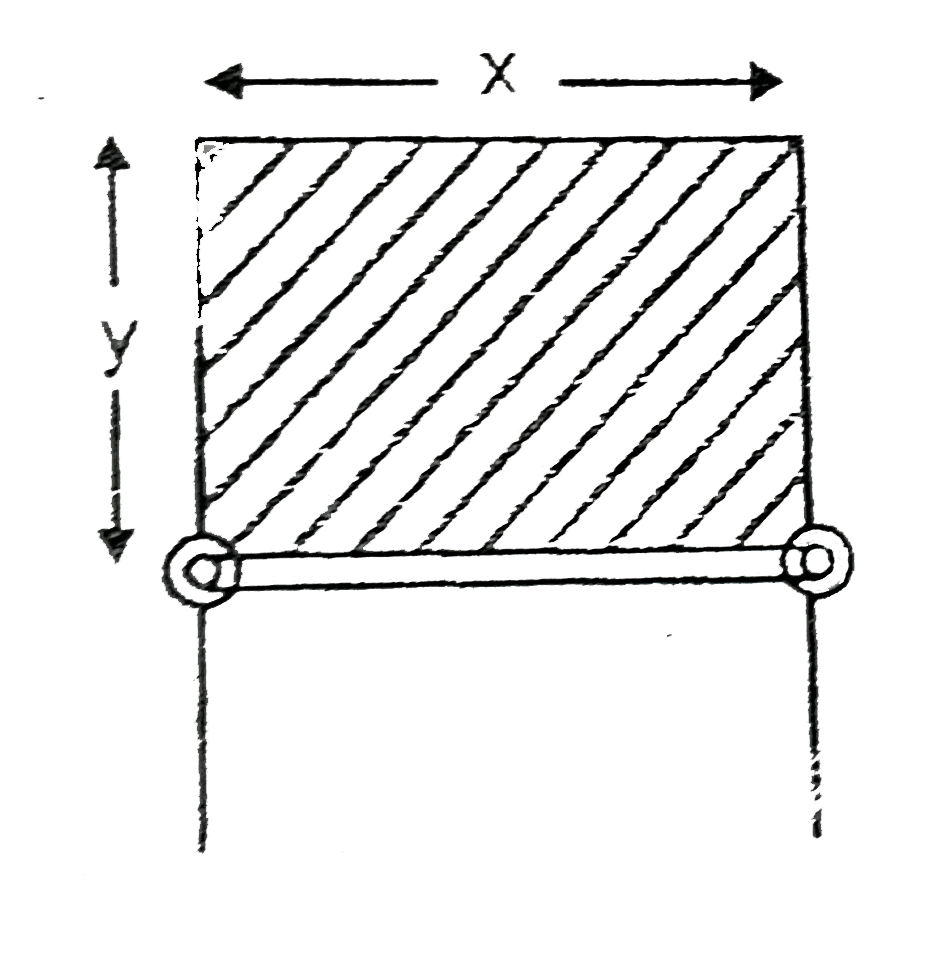
Between a frame and a light slider, a thin film of soap solution is made. Whose length is x and width is y. Find surface tension force on the slider. To keep the slider in equilibrium, how much weight should be suspended ?
View Solution_E01_194_Q01.png)
PQRS is a rectangular frame of copper wire shown in figure the side RS of the frame is movable. If a soap film is formed on it then what is the diameter of the wire to maintain equilibirum (given surface tension of soap solution =0.045N/m and density of copper =8.96×103kg/m3)
View Solution
Knowledge Check
U - shaped film of a liquid is formed between a wire frame and movable wire 5 cm long. Then the force required to hold the wire in equilibrium is ,
(Surface tension of liquid is 0.024 N/m )A2.4×10−3 NB24×10−3 NC2.4×10−3 dyneD2.4×10−3 dyne/cmA liquid film is formed over a frame ABCD as shown in figure. Wire CD can slide without friction. The mass to be hung from CD to keep it in equilibrium is
 ATlgB2TlgCg2TlDT×l
ATlgB2TlgCg2TlDT×lA 10 cm long wire is placed horizontal on the surface of water and is gently pulled up with a force of 2×10−2 N to keep the wire in equilibrium. The surface tension, in Nm−1 of water is
A0.1B0.2C0.001D0.002
A soap film is formed on a rectangular frame of length 7 cm dipping in soap solution. The frame hanges from the arm of a balance. An extra weight of 0.38 g is to be placed in the opposite pan to balance the pull on the frame. Calculate the surface tension of the soap solution. Giveng=980cms−2.
View SolutionA wire of length 10 cm and area of cross section 1mm2 has a resistance of 5Ω. Find the resistivity of the material of the wire.
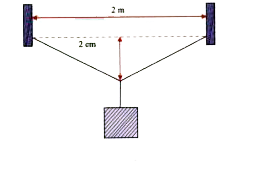
View SolutionA wire of length 2 m is fixed, as shown. When a load is suspended from the center, it sags by 2 cm. Find the strain.
View SolutionA wire 10 cm long is placed horizontally on the surface of water. It is gently pulled up with a force of 1.4×10−2 N to keep It in equilibrium . The surface tension of water is
View SolutionA film of soap solution is formed in a rectnagular wire frame of length 10 cm and breadth 5 cm . The surface energy of the film , if the surface tension of soap solution is 0.035 N/m is
View Solution
