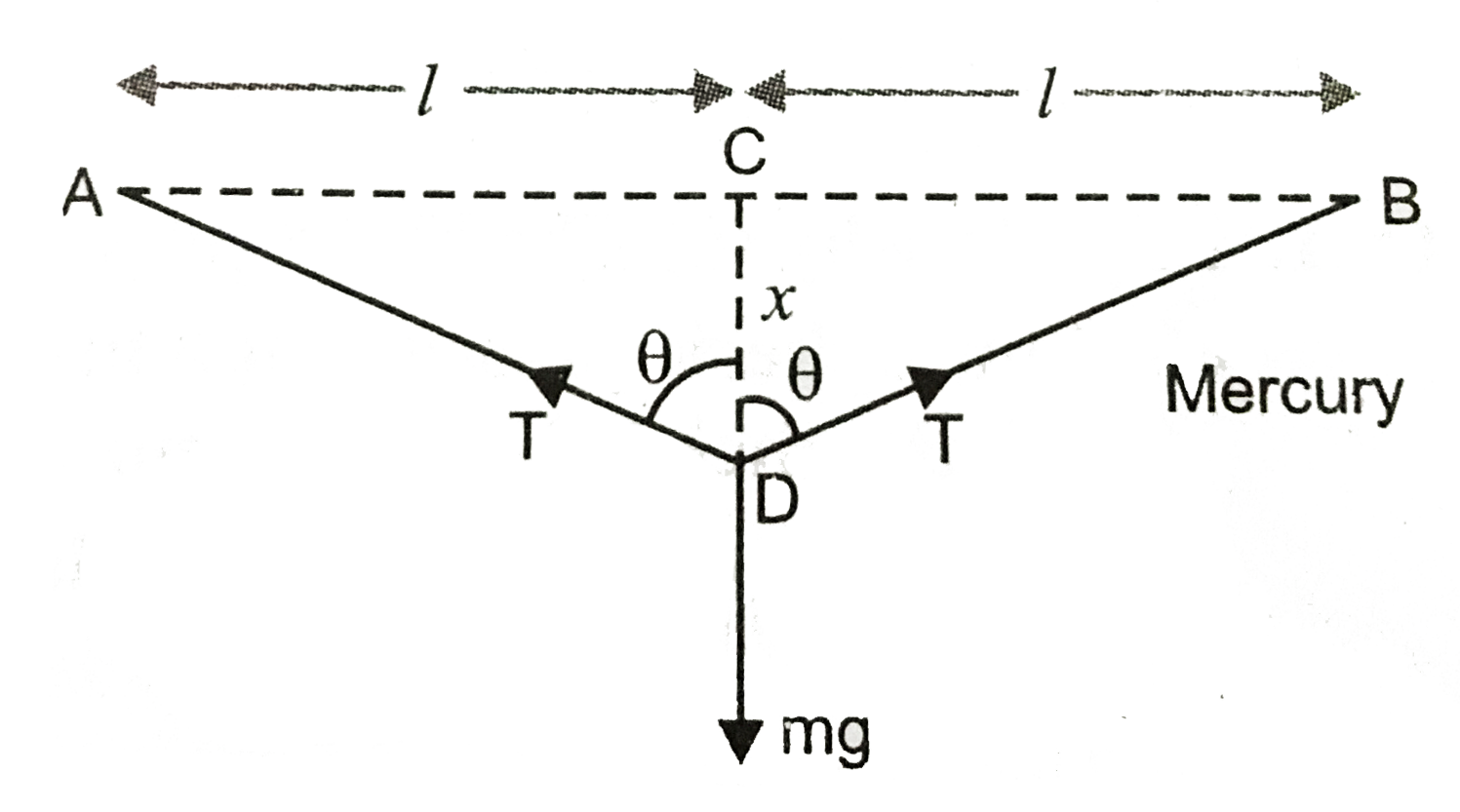
A steel wire of original length 1 m and cross-sectional area 4.00 mm^2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ?
Yofthesteel=2.0x10^11Nm^-2. Take g=10ms−2
The correct Answer is:A, C
From cosθ=X√X2+I2
=XI{1+X2I2}−12
=X.I….1
increase in length
ΔL=(AC+CB)−AB
here AC=(I2+X2)^(1/2)
So, ΔL=2(I2+X2)120
given that A=4mm2
=4×10−2cm2
Substituing the values we have
Y=FALΔL
→2×10612
=T×100(4dxx10−2)×[2(502+X2)12−100]........2
from equation i, ii and the freebody diagram ltbr> 2Tcosθ=mg
2T(X50)=2.16×103×980
=2×(2×1012)×(4×10−2)×[2(502+X212)−100×X]100×50
(2.16)×103×980
Solving for X, we get X=1.5 cm.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective 2
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
Similar Questions
A mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
View SolutionA mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View Solution
Knowledge Check
A mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
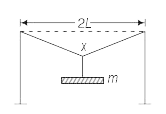 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
Ax22L2BxLCx2LDx22LA mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
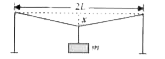
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22L
A steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceilign and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionA steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel =2×1011N/m2)
View SolutionA steel wire of negligible mass, length 2I, cross sectional area 'A' and Young's modulus 'Y' is held between two rigid walls. A small body of mass 'm' is suspended from its middle point 'O' as shown. The vertical descent of the middle point 'O' of the wire is

View SolutionAn aluminum wire and a steel wire of the same length and cross-section are joined end to end. The compoiste wire is hung from a rigid support and a load is suspended from the free end. If the length of the composite wire is 2.7mm then the increases in the length of wire is (in mm)
(YAl=2×1011Nm2,YSteel=7×1011Nm−2)
View Solution
