A uniform horizontal rod of length 40 cm and mass 1.2 kg is supported by two identical wires as shown in figure. Where should a mass of 4.8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone ? Take g=10ms−2

The correct Answer is:5cm
Length of the rod, L=40cm=0.4m
mass of the rod =m=1.2kg
let the 4.8 kg mass be placed at a distance x from the left end.
Given fd=2f2
∴12L√T1m=22L√T2m
→√T1T2=2
→T1T2=4.
From the free body diagram
T1+T2=48+12=60N
→4Tr+Tr=5Tr=60N
∴Tr=12N
andT1=48N
now taking moment about point A
Tr×(0.4)=48x+12(0.2)
→4.8=48x−2.4
→4.8x=2.4
−x=2448=120m=5cm
so, the mass should be placed at a distance 5 cm from tehleft end.
Topper's Solved these Questions
Similar Questions
A uniform horizontal rod of length 40cm and mass 1.2kg is supported by two identical wires as shown in figure. Where should a mass of 4.8kg be placed on the ord form left end (in cm) so that the same tuning fork may excite the wire on left into its fundament vibrations and that on right into its first overtone? Take g=10m/s2.

View SolutionA metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View Solution
Knowledge Check
A straight horizontal conducting rod of length 50 cm and mass 50 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (take=10ms−2
A0.05TB0.1TC0.2TD0.5TA horizontal rod of length 5m weight 4 kg is suspended at the ends by two strings. The weights 8 kg, 12 kg, 16 kg and 20 kg are placed on the rod at distance 1 m, 2 m, 3 m and 4 m from one end of the rod. Then the tensions in the string are
A26, 34 kg. wt.B20, 30 kg. wtC10, 40 kg. wt.DNone of these
A straight horizontal conducting rod of length of 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order that the tension in the wire is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires) g=9.8ms−2
View SolutionA straight horizontal conducting rod of length 0⋅60m and mass of 60g is suspended by two vertical wires at its ends. A current of 5⋅0A is set up in the rod through the wire. (a) What magnetic field should be set up normal to the conductor in order that the tension in the wire is zero?
(b) What will be total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before (Ignore mass of the wire), g=10ms−2.
View SolutionA straight horizontal conducting rod of length 0⋅45m and mass 60g is suspended by two vertical wires at its end. A current of 5⋅0A is set up in the rod through the wires. (a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (b) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before. (Ignore the mass of the wire) g=9⋅8ms−2.
View SolutionA uniform rod of the length of 1 m and mass of 2 kg is attached to side support at O as shown in the figure. The rod is at equilibrium due to upward force T acting at P . Assume the acceleration due to gravity as 10ms−2 The value of T is
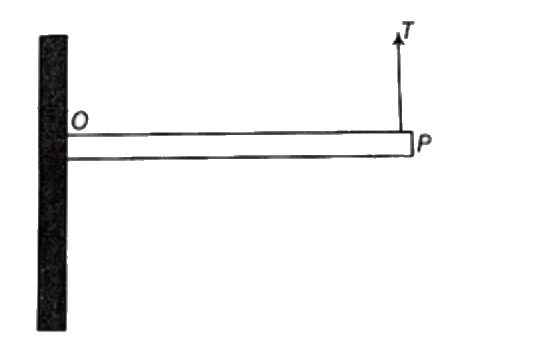
View SolutionA sonometer wire has a length of 114 cm between its two fixed ends. Where should the two briges be places so as todivide the wire into three segments, whos fundamental frequencies are in the ratio 1:3:4?
View SolutionA conducting rod of 1 m length and 1 kg mass is suspended by two vertical wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now, the current to be passed through the rod so as to make the tension in the wires zero is : (Take g=10ms−2) :
View Solution
