A 2.00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
The correct Answer is:A, B, C
L=length of rope =2m,
M=mass=80gm
=0.08kg
mass per unit length =m
=0.082=0.04kgm
Tension , T=256N
Velocity , V=√(Tm)
=√(256004)=1602=80ms
For fundamental frequency
I=λ4
→λ=4I=4×2=8m
→f=808=10Hz
a. therefore, the frequency of 1st two overtones are
1st overtone =3f=30 Hz
2nd overtone =5f=50Hz.
b. λ=4I=4×2=8m
∴λ1=Vf1=8030=2.67m
λ2=Vf2=8050=1.6m
So the wavelength are 8, 2.67m and 1.6m respectively.
Topper's Solved these Questions
Similar Questions
A 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionA 160 g rope 4 m long is fixed at one end and tied to a light string of the same length at the other end. Its tension is 400 N.
(a) What are the wavelength of the fundamental and the first two overtones?
(b) What are the frequencies of these standing waves?
[Hint : In this case, fixed end is a node and the end tied with the light string is antinode.]
View Solution
Knowledge Check
A string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
AL4BL2CLD2LA body of mass 100g is tied to one end of a 2m long string. The other end of the string is at the centre of the horizontal circle. The maximum revolution in one minute is 200. The maximum tensible strength of the string is approx
A8.76 NB8.94 NC89.42 ND87.64 NA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.
 AMLB2MLC4MLD16ML
AMLB2MLC4MLD16ML
A steel wire of mass 4.0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
View SolutionA 20cm long string, having a mass of 1.0g, is fixed at both the ends. The tension in the string is 0.5N. The string is into vibrations using an external vibrator of frequency 100Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA 20 cm long string, having a mass of 1.0 g, is fixed at both the ends. The tension in the string is 0.5 N. The string is set into vibrations using an external vibrator of frequency 100 Hz. Find the separation (in cm) between the successive nodes on the string.
View SolutionA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
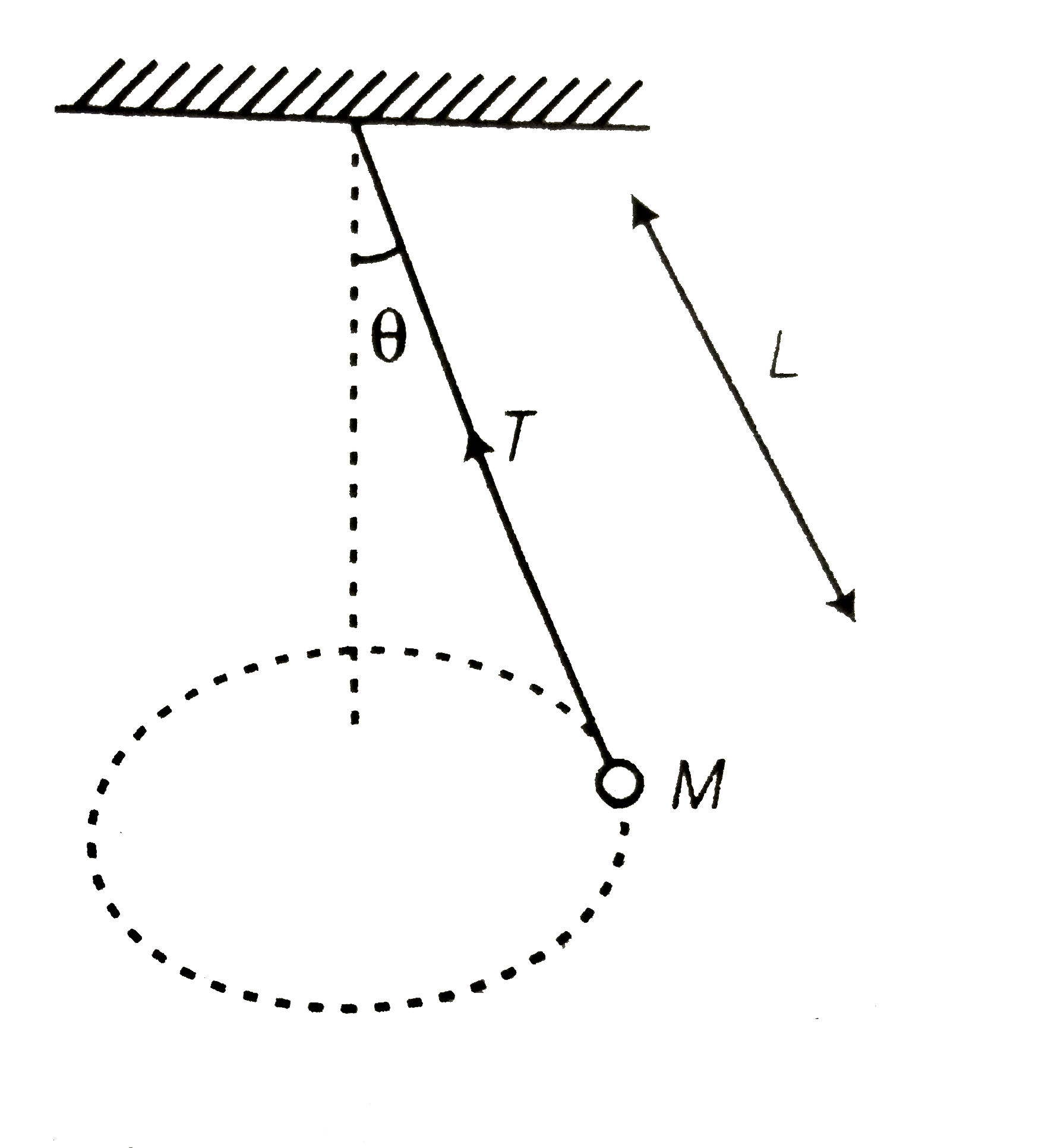
View SolutionA string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
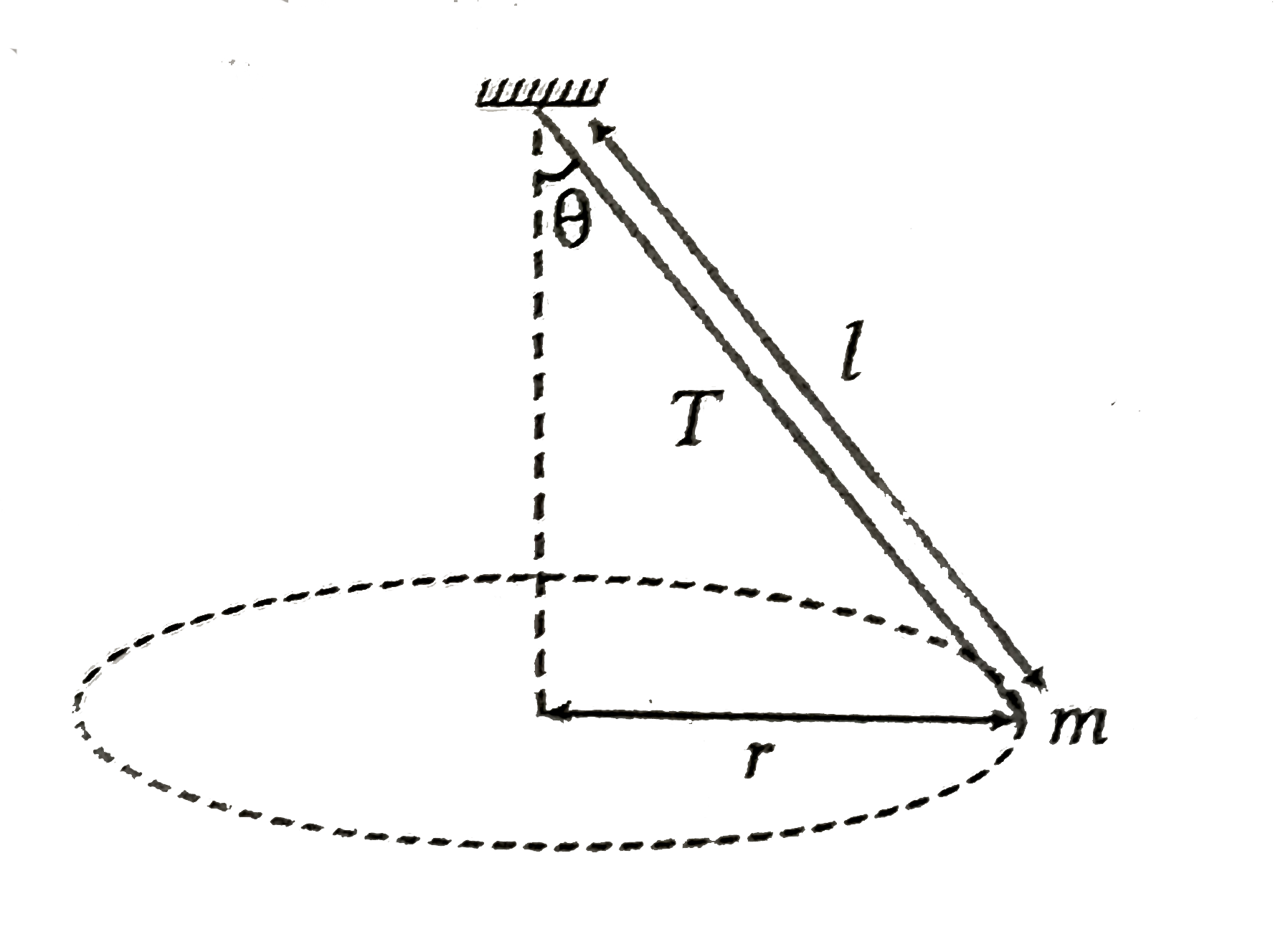
View Solution
