A uniformly charged thin spherical shell of radius R carries uniform surface charge denisty of isgma per unit area. It is made of two hemispherical shells, held together by presisng them with force F(see figure). F is proportional to

1ε0σ2R2
1ε0σ2R
1ε0σ2R
1ε0σ2R2
The correct Answer is:A
The charge on the sphere is
= Area × surface charge density
=4πR2×σ
Therefore for the hemisphereical
shell, charges (q)=2πR2σ
The intensity of the electric field near a conductor is
E=σ2ε0 butE=Fq
F=Eq=(σ)(2ε0)×2πR2σ=πσ2R2ε0
∴F∝σ2R2ε0
Topper's Solved these Questions
Similar Questions
A uniformly charged thin spherical shell of radius R carries uniform surface charge density of sigma per unit area.It is made of two hemispherical shells hold together by pressing them with force F.F is equal to qquad F + + +(1)/(+)+
View SolutionA spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
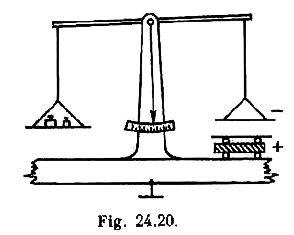 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The electric field inside a spherical shell of uniform surface charge density is
AZeroBConstantCProportional to the distance from the centreDIrregular - Question 2 - Select One
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2 - Question 3 - Select One
Two uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:
 AQ1BQ2CRDr
AQ1BQ2CRDr
A uniformly charged thin conducting spherical shell of radius R and charge q is rotated with constant angular velocity ω about a diameter. The magnetic dipole moment of the system is
View Solution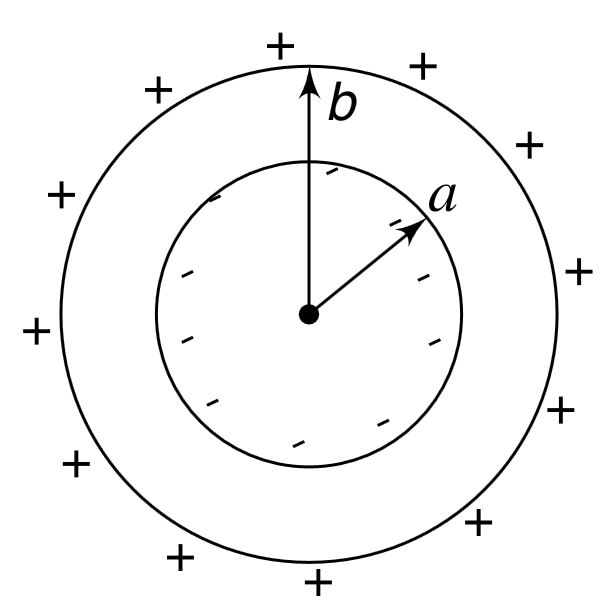
A thick conducting spherical shell of inner radius a and outer radius b is shown in figure. It is observed that the inner face of the shell carries a uniform charge density −σ. The outer surface also carries a uniform surface charge density +σ.
(a) Can you confidently say that there must be a charge inside the shell? Find the net charge present on the shell. (b) Find the potential of the shell.View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.View SolutionA spherical shell of radius r carries a uniformly distributed surface charge q on it. A hemispherical shell of radius R(gt r) is placed covering it with its centre coinciding with that of the sphere of radius r. The hemisphere has a uniform surface charge Q on it. The charge distribution on the sphere and the hemisphere is not affected due to each other. Calculate the force that the sphere will exert on the hemisphere.
 View Solution
View SolutionConisder a thin spherical shell of radius R with centre at the origin, carrying uniform poistive surface charge denisty. The variation of the magnitude of the electric field ∣∣→E(r)∣∣ and the electric potential V(r) with the distance r from the centre, is best represented by which graph?
View Solution

