For the following linear programming problem minimize Z=4x+6y subject to the constraints 2x+3y≥6,x+y≤8,y≥1,x≥0, the solution is

A

(0, 2) and (1, 1)

B

(0, 2) and (32,1)

C

(0, 2) and (1, 6)

D

(0, 2) and (1, 5)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Given, Z=4x+6y
The minimum point of Z can be on
A, B, C and D.
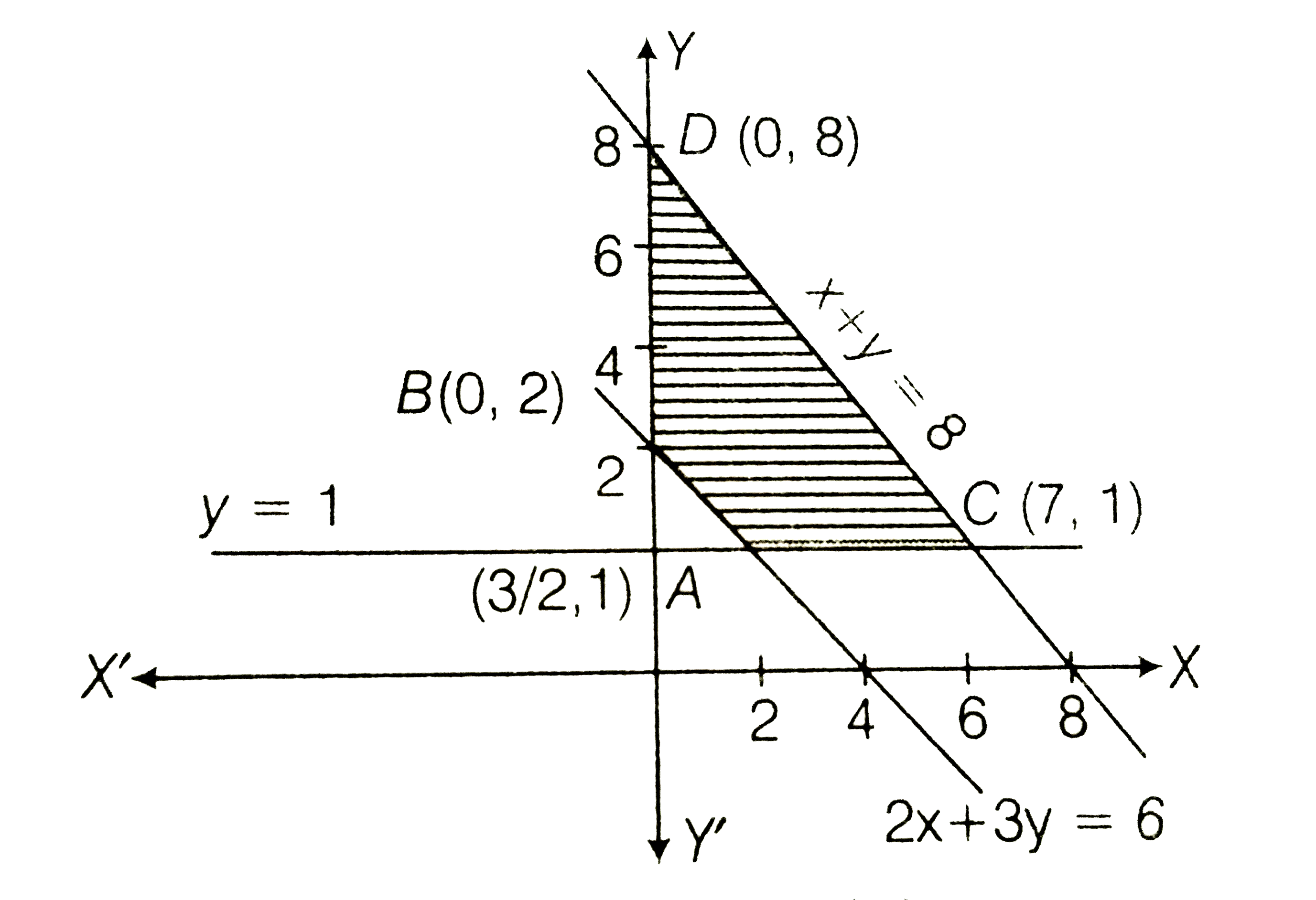
ocr_image
Now, ZA=Z(3/2,1)=4(32)+6(1)
=6+6=12
ZB=Z(0, 2)=4(0)+6(2)
=0+12=12
ZC=Z(7, 1)=4(7)+6(1)
=28+6
=34
and ZD=Z(0, 8)=4(0)+6(8)
=0+48=48
∴ Z minimum at the point (32,1) and (0, 2).

Updated on:21/07/2023
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • maximize z=60x+15y, subject to the constraints x+y≤50,3x+y≤90,x,y≥0.

    AThe maximum value of z is at C(40,0).
    BThe maximum value of z is at C(30,0).
    CThe maximum value of z is at C(50,0).
    DThe maximum value of z is at C(60,0).

  • The maximum value of z = 4x +2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is

    A36
    B40
    C20
    DNone of these

  • The minimum value of z = 3x + y subject to constraints 2x+3y≤6,x+y≥1,x≥1,x≥0,y≥0 is

    A0
    B3
    C2
    D1