If given constraints are 5x+4y≥2,x≤6,y≤7, then the maximum value of the function z=x+2y is
A
13
B
14
C
15
D
20
Video Solution
Text Solution
The correct Answer is:D
Feasible region is ABCDEA and Z=x+2y .
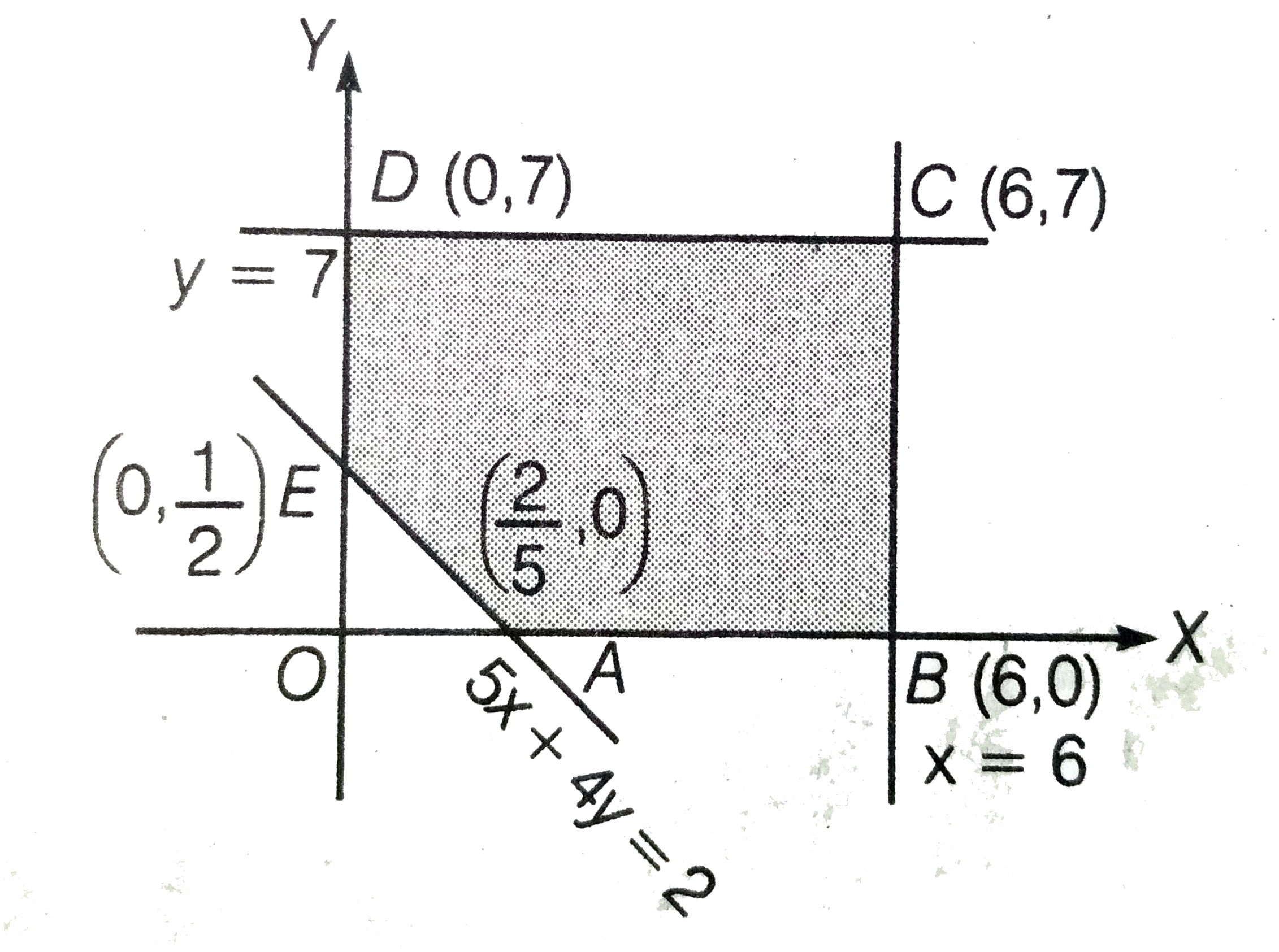
At point A (2/5 , 0) Z=25+0=25
At point B (6,0) Z =6 +0=6
At point c(6,7), Z =6+14 = 20 (max.)
At point D(0,7) Z=0+2(7)=14
At point E(0,12)Z=0+2(12)=1
∴ Maximum vlaue of Z is 20.
|
Topper's Solved these Questions
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )
30 Videos
- LINEBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner
3 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
Similar Questions
Knowledge Check
If Z=2x + y subject to x≤4,y≤6,x+y≥6,x≥0,y≥0, then the maximum value of Z is
A18B10C6D14Consider the linear programming problem Maximise Z = 4x + y.
Subject to constraints x+y≤50,x+y≥100 and x,y≥0 Then, maximum vlaue of Z isA0B50C100Ddoes not exist
2x+y≥4,x+y≤3,2x−3y≤6
View Solution2x+y≥4,x+y≤3,2x−3y≤6
View SolutionFor the system for linear inequations x+y≤6,3x+5y≥15,x≥0,y≥0, If Z=3x+2y, then the maximum value of Z occurs at :
View SolutionMaximize if possible:
(i) Z=3x+2y subject to the constraints:
x−y≤1,x+y≥3,x≥0,y≥0
(ii)Z=3x+4y subject to the constraints :
x−y≤−1,−x+y≤0,x≥0,y≥0.
View Solutionx−2y≤2,x+y≤3,−2x+y≤4,x≥0,y≥0
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View Solution
