यदि x+y=1 तो फलन xy2 का उच्चिष्ट मान ज्ञात कीजिए ।
माना P=xy2
=x(1−x)2
dPdx=x[2(1−x)(−1)]+(1−x2)(1)
=−2x(1−x)+(1−x)2
(1−x)(−2x+1−x)
(1−x)(1−3x)
P के उच्चिष्ट या nmnisht मान के लिए dPdx=0
∴ (1−x)(1−3x)=0
x=1,13
अब d2Pdx2=(1−x)(−3)+(1−3x)(−1)
=−3+3x−1+3x
=6x−4
अब x =1 के लिए
d2ydx2=6−4
अब x=1के लिए
d2ydx2=6−4
=2
= धनात्मक राशि
∴x=1 पर P का मान निम्निष्ट है।
अब x=13के लिए, d2ydx2=6×13−4
=2−4
=−2
ऋणात्मक राशि
∴x=13 का मान उच्चिष्ट है।
∴ फलन का उच्चिष्ट मान =13(1−13)2
=13(23)2
=13×49=427
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionयदि 2x+y=1 तो फलन x2y का उच्चिष्ठ मान ज्ञात कीजिए
View Solutionयदि (cosx)y =(sin y) ^(x) , तो(dy)/(dx) का मान ज्ञात कीजिए|
View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
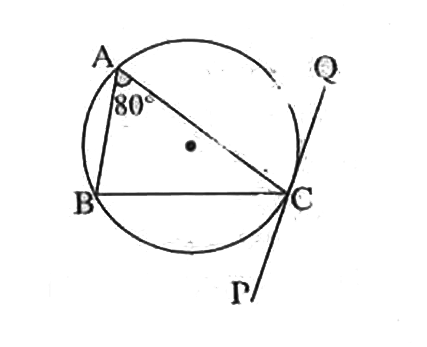
View Solutionफलन 3 sin x +4 cos x का उच्चिष्ठ मान ज्ञात कीजिए।
View Solutionयदि xy = 4 तथा x> 0 तो x का वह मान ज्ञात कीजिए जिसके लिए x + y न्यूनतम है।
View Solutionयदि y=1−cos2x1+cos2x है तो dydx का मान ज्ञात कीजिए।
View Solutionयदि y=cot(cos−1x) है तो dydx का मान ज्ञात कीजि।
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=(2x−1)2+3
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=−(x−1)2+10
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
View Solution
