सिद्ध कीजिए की वृत के अंतग्रत महत्तम क्षेत्रफल वाला आयत एक वर्ग है।
मानलो की वृत का केंद्र मूलबिंदु और वृत की त्रिज्या a है।
∴वृत का समीकरण x2+y2=a2
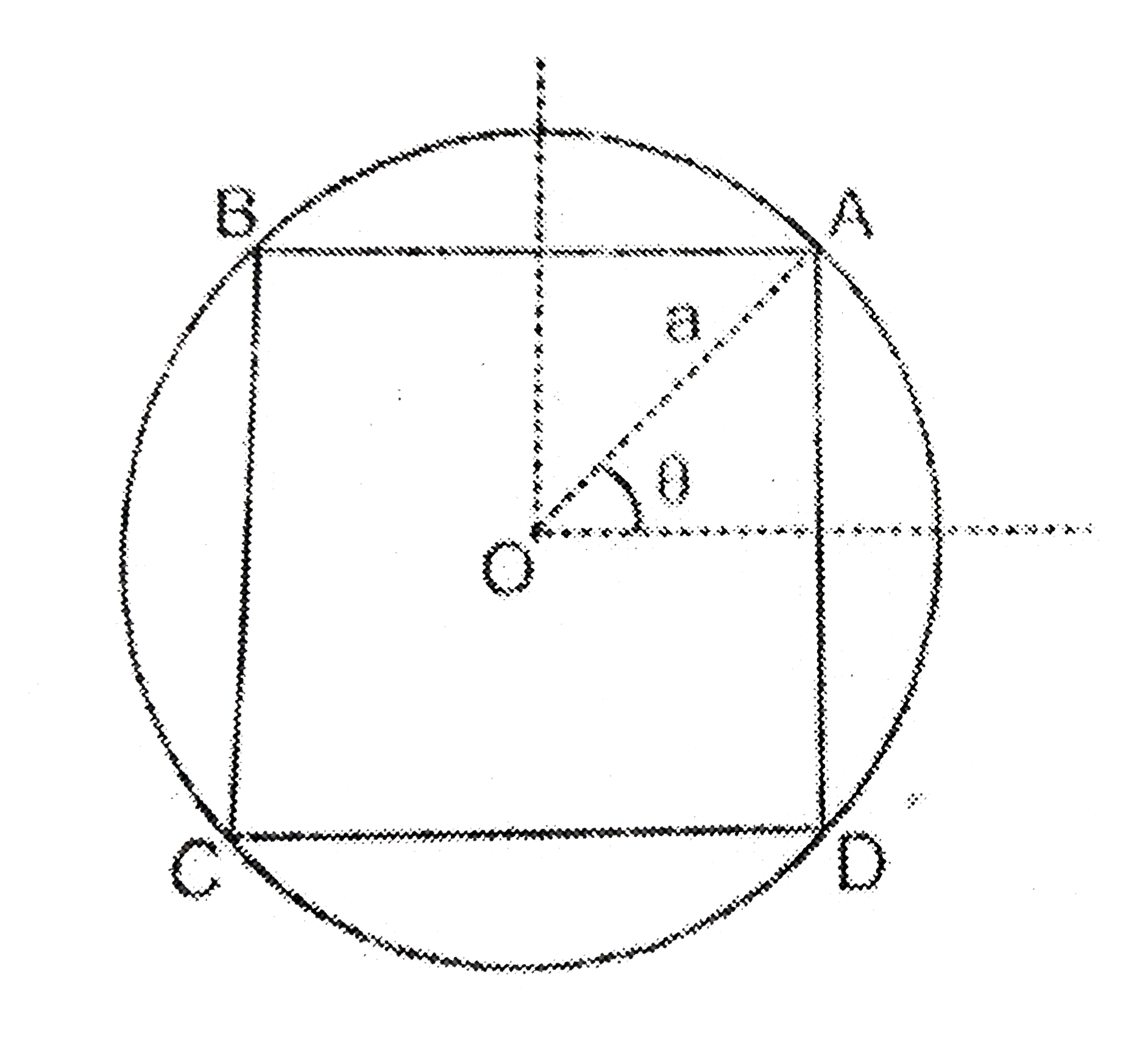
वृत्त के अंतग्रत एक आयत ABCD है स्पष्टतः A के निर्देशांक (acos0,asin0) है। मान लीजिए आयत का क्षेत्रफल S है, तो
S=AB×AD
=2asin0,2acos0
2a2sin20
अब अवकलन करने पर dSd0=0प्रतिस्तापित करने पर
4a2cos20=0 या cos20=0=cosπ2
⇒ 20=π2 या 0=π4
पुनः अवकलन करने पर,
d2Sd02=−4a22sin20=−8a2sin20
∴0=π4रखने पर ltbgt d2Sd02=−8a2sin2(π4)=−8a2sinπ2=−8a2ऋणात्मक
∴जब 0=π4,AB=2asin0=2asinπ4=√2a
और AD=2acos0=2acosπ4=√2a ∴AB=AD अतः जब आयत का क्षेत्रफल उच्चिष्ट होगा तब आयत एक वर्ग है।
दूसरी विधि - मान लीजिए की आयत की भुजाये x तथा y है। A उसका क्षेत्रफल है और वृत की त्रिज्या a है।
∴ A=xy
और वृत का समीकरण x2+y2=a2
समीकरण (i ) और (ii ) से
A=x√a2−x2
A महत्तम होगा जब dAdx=0और d2Adx2=−ve (ऋणात्मक )
अब dAdx=√a2−x2।1+x12(a2−x2)−1/2(−2x)=0
⇒ a2−x2−x2√a2−x2=0∴x=±a√2
⇒ x=a√2
और d2Adx2=(√a2−x2(−4x)−(a2−2x2))⋅12(a2−x2)−1/2(−2x))a2−x2
d2Adx2 का मान x=a√2 के लिए ऋणात्मक है।
∴ जब x=a√2,y=√a2−x2=√a2−a22=a√2
अतः क्षेत्रफल महत्तम होगा जब x =y अर्थात आयत एक वर्ग होगा।
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionएक आयत की भुजाएँ x=2,x=−4,y=3 और y=−5 है। इसके विकर्णों के समीकरण ज्ञात कीजिए ।
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionसमतल आकृतियाँ |आयत ,वर्ग वृत्त तथा त्रिभुज #!#परिमाप और क्षेत्रफल
View SolutionThe area of square is 200m^2 . A new square is formed in such a way that the length of its diagonal is sqrt2 times of the given square. Then the area of the new square formed is- एक वर्ग का क्षेत्रफल 200 वर्ग मीटर है। एक नया वर्ग इस प्रकार बनाया गया है कि उसके विकर्ण की लंबाई पहले वर्ग के विकर्ण की sqrt2 गुना के बराबर है, नये वर्ग का क्षेत्रफल है-
View SolutionThe perimeter of a rectangle is 50 cm. Its area and length are in the ratio of 5:1. Find the length of the rectangle?
एक आयत की परिधि 50 सेमी है। इसका क्षेत्रफल और लंबाई 5: 1 के अनुपात में है। आयत की लंबाई ज्ञात कीजिये?
View SolutionIf the perimeter and length of a rectangle are in the ratio 6:1 and the area of the rectangle is 288cm2. Find the length of the rectangle.
यदि आयत की परिधि और लंबाई 6: 1 के अनुपात में है और आयत का क्षेत्रफल 288 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।
View SolutionThe length of the diagonal of a rectangle is 26 cm and one side is 10 cm. The area of the rectangle is:
एक आयत के विकर्ण की लंबाई 26 सेमी है तथा इसकी एक भुजा 10 सेमी की है | इस आयत का क्षेत्रफल है:
View SolutionThe length of a rectangle is 6 cm more than its breadth. And its perimeter is 100 cm. If the area of this rectangle is nearest equal to the area of a circle, then what will be the circumference of this circle ?
एक आयत की लम्बाई, उसकी चौड़ाई से 6 cm अधिक है और उसका परिमाप 100 cm है | यदि इस आयत का क्षेत्रफल एक वृत्त के क्षेत्रफल के निकटतम बराबर है, तो उस वृत्त की परिधि कितनी है?
View SolutionThe perimeter and length of a rectangle are in the ratio of 8:1, and the area of the rectangle is 1323cm2. Find the length of the rectangle.
एक आयत का परिमाप और उसकी लंबाई 8:1 के अनुपात में है। आयत का क्षेत्रफल 1323 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।
View SolutionThe breadth of a rectangle is four times of its length. If the area of the rectangle is 1764, then what is the breadth of the rectangle? एक आयत की चौड़ाई इसकी लंबाई का चार गुना है। यदि आयत का क्षेत्रफल 1764 है, तो आयत की चौड़ाई क्या है?
View SolutionIf the breadth and perimeter of a rectangle are in the ratio 1:8 and the area of rectangle is 363 cm^3 , then the breadth of the rectangle is: यदि आयत की चौड़ाई और परिधि 1:8 के अनुपात में है और आयत का क्षेत्रफल 363 cm^3 है, तो आयत की चौड़ाई है
View Solution
