दिखाइए की एक समकोण वृताकार शंकु के अंतर्ग्रत बने सबसे बढ़े बेलन का आयतन 427πh3tan2aहै जबकि शंकु की ऊंचाई h और अर्ध शीर्षकोण a है।
ज्ञात है की AO = h और ∠BAO=a
मानलो की वेलन की त्रिज्या x है
∴ΔAPOसे, AO'=xcota
∴ OO'=बेलन की ऊंचाई =h−xcota
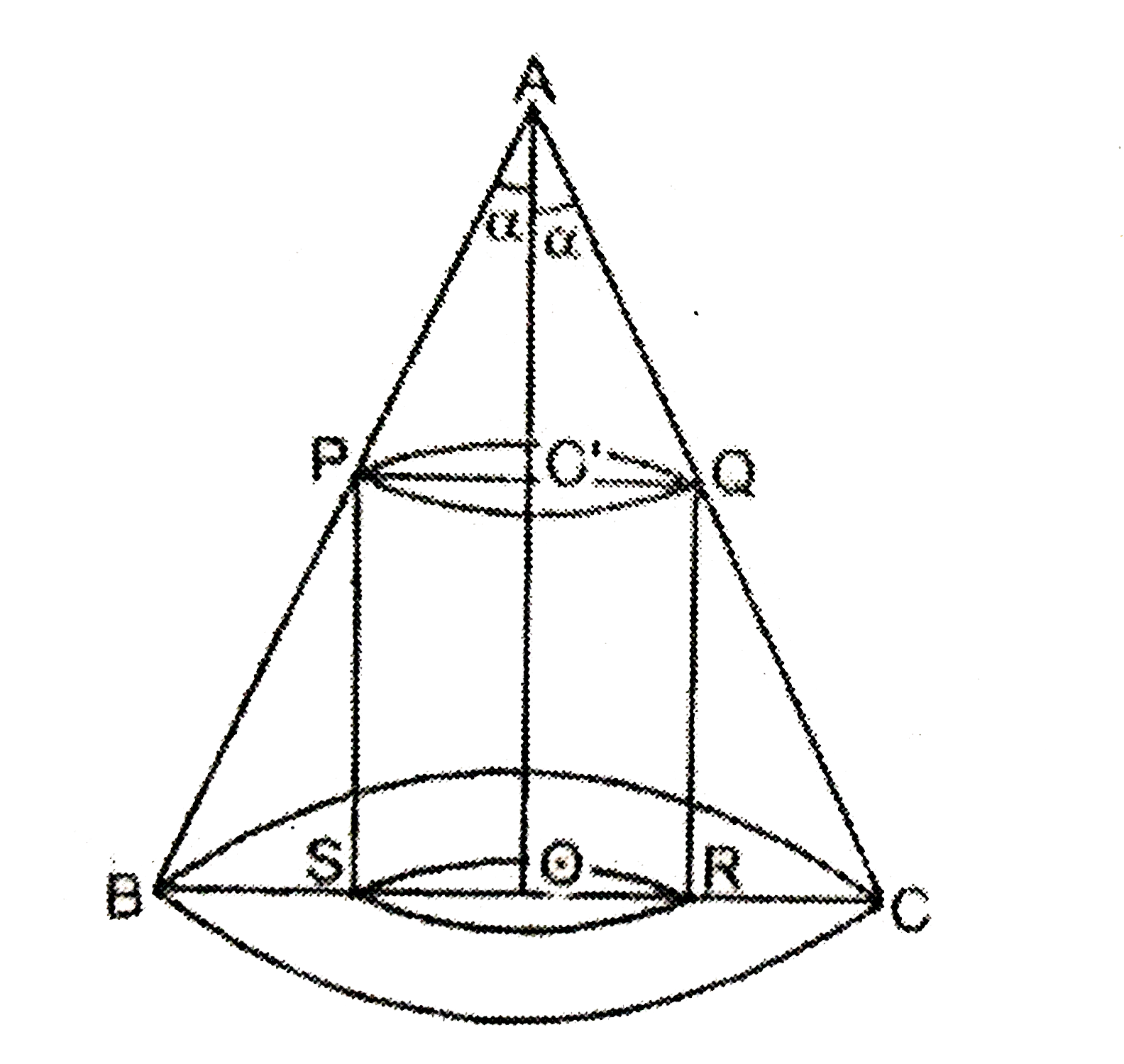
∴ बेलन का आयतन V=πx2(h−xcota)V=π(x2h−x3cota)
अब आयतन महत्तम हो जब
dVdx=0और d2Vdx2=−ve ऋणात्मक
समीकरण (1 ) का x के सापेक्ष अवकलन करने पर,
dVdx=π(2xh−3x2cota)
dVdx=0 प्रतिस्थापित करने पर
π(2xh−3x2cota)=0 या 2h−3xcota=0∵x≠0ltBRgt ∴ x=2h3cotα
अब d2Vdx2=π(2h−6xcotα)
x=2h3cotα प्रतिस्तापित करने पर
d2Vdx2=π(2h−62h3cotαcotα)=π(2h−4h)
=−2πh, जो ऋणात्मक है।
अतः आयतन महत्तम है जब x x=2h3cotα
∴ " " अभीष्ट महत्तम आयतन =πx2(h−xcotα)
π4h29cot2α(h−2h3),
=π4h29cot2α×h3=427πh3tan2α)
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionबेलन का आयतन|उदाहरण#!#शंकु का आयतन
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृष्ठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View SolutionThe numerical values of the volume and the area of the lateral surface of a right circular cone are equal if the height of the cone be h and radius be r, the value of 1/h^2+1/r^2 is- एक लंब चृत्तीय शंकु के आयतन और क्षेत्रफल पारश्वीय पृष्ठ के संख्यात्मक मान समान है। यदि शंकु की ऊंचाई h और त्रिज्या r है, तो 1/h^2+1/r^2 का मान है-
View SolutionThe radii of two circular faces of the frustum of a cone of height 21 cm are 3 cm and 2 cm respectively. What is the volume of the frustum of the cone in cubic cm? (Take π=227)
21 सेमी ऊंचाई वाले शंकु के छिन्नक के दो वृताकार फलकों की त्रिज्या क्रमशः 3 सेमी और 2 सेमी है। घन सेमी में शंकु के छिन्नक का आयतन कितना होगा ?
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View SolutionIf the radius of the base of a cone is doubled, and the volume of the new cone is three times the volume of the original cone, then what will be the ratio of the height of the original cone to that of the new cone ?
यदि किसी शंकु के आधार की त्रिज्या दोगुनी कर दी गयी है , और नए शंकु का आयतन आरंभिक शंकु के आयतन का तिगुना है, तो आरंभिक शंकु और नए शंकु की ऊँचाइयों के बीच क्या अनुपात होगा ?
View SolutionRadius of the base of a right circular cone and a sphere is each equal to r. If the sphere and the cone have the same volume, then what is the height of the cone?
एक लम्ब वृत्तीय शंकु के आधार एवं एक गोले की त्रिज्या दोनों r के बराबर है | यदि गोले और शंकु का आयतन समान है, तो शंकु की ऊंचाई कितनी है ?
View Solution
