यदि एक समकोण त्रिभुज के कर्ण और एक भुजा की लम्बाइयों का योग दिया हो, तो दर्शाइये कि त्रिभुज क्षेत्रफल महत्तम होगा यदि इन भुजाओं के बीच का कोण हो।
मानलो दिया हुआ त्रिभुज ABC है जो B पर समकोण है तथा इसकी भुजा AB और कर्ण AC का योगफल दिया हुआ है तथा यह योगफल P है। अब यदि AB =c तो
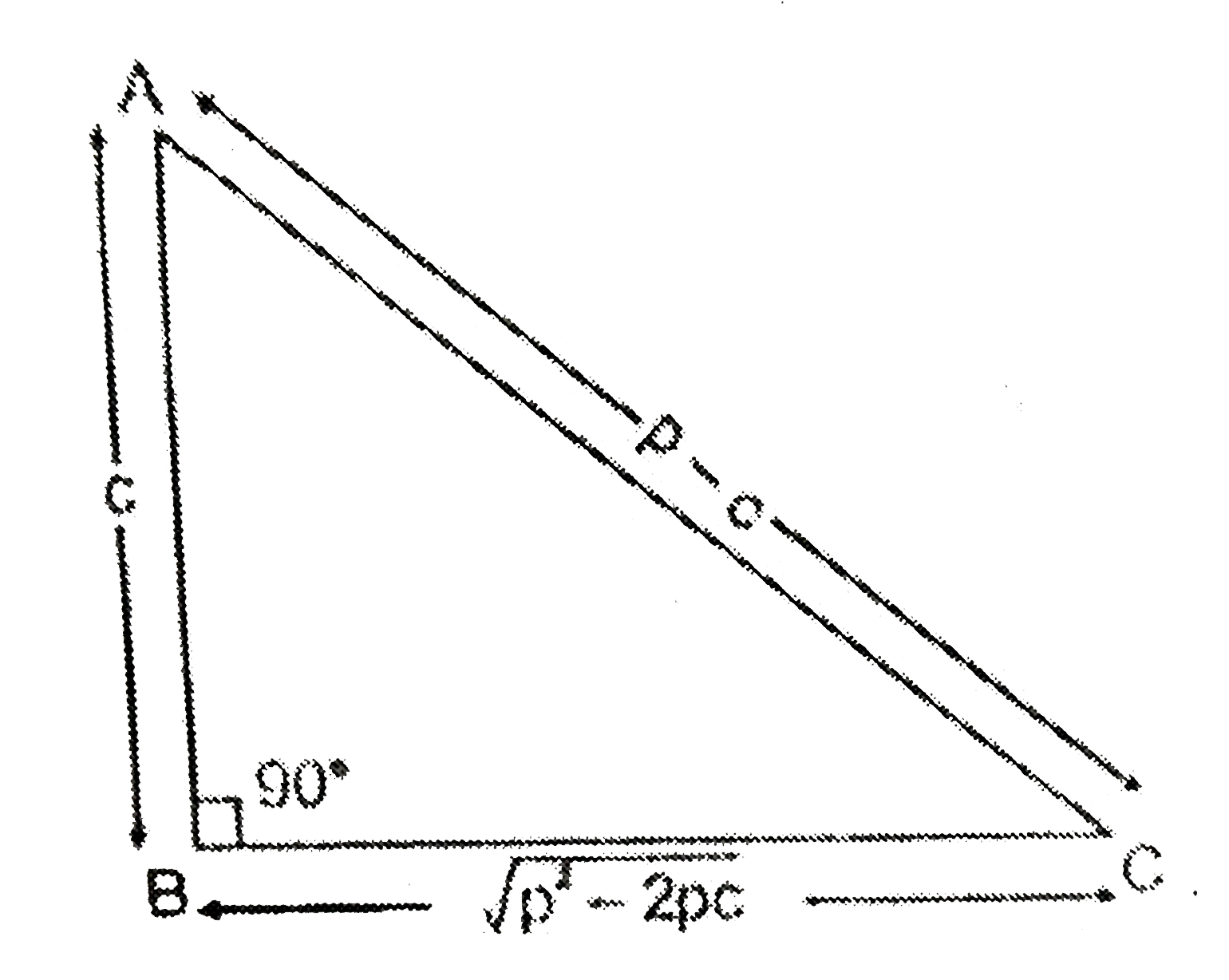
आधार
अतः का
यदि क्षेत्रफल S है तो
स्पष्टः S चर राशि c का फलन है।
अब p उचिष्ट अथवा निनिष्ट होगा जबकि
अथार्त जब
या या अथवा p =3c
से त्रिभुज का बनना असम्भव है। अतः p =3c पुनः जब p =3c तो
जो ऋणात्मक है अतः जब p =3c तो त्रिभुज के क्षेत्रफल का मान उचिष्ट होगा।
पुनः जब p =3c तो,
तथा
अतः जब प्रश्न में वर्णित भुजाओ के बीच कोण होगा तो त्रिभुज क्षेत्रफल उच्चतम होगा।
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionत्रिभुज ABC में कोण C समकोण है । यदि बिंदु A और B निर्देशांक क्रमशः (−3,4) और (3,−4)हो , तो सिद्ध कीजिये की ΔABC के परिवृत्त का समीकरण x2+y2=25 होगा ।
View Solutionयदि ¯a और ¯b दो मात्रक सदिश हों, तो ¯a और ¯b के बीच का कोण क्या होगा, यदि ¯a−√2¯b एक मात्रक सदिश हो ?
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionयदि →a−→b=→O हो , तो →aऔर→b के बीच का कोण ……………. होगा।
View Solutionयदि →a=ˆi+2ˆj+2ˆk,∣∣→b∣∣=5 और →a तथा→b के बीच कोण π6 है , तब दोनों भुजाओं के रूप में इन दो सदिशों के द्वारा बनने वाले त्रिभुज का क्षेत्रफल है -
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionएक त्रिभुज का क्षेत्रफल
View Solutionएक त्रिभुज की रचना|जब दो कोण एवं तीनों भुजाओं का योग दिया हो
View Solution
