सिद्ध कीजिए की दिए हुए सम्पूर्ण पृष्ट और अधिकतम आयतन वाले बेलन की ऊंचाई आधार के व्यास के बराबर होती है।
मानलो बेलन के आधार की त्रिज्या r तथा ऊंचाई h है। उसका सम्पूर्ण पृष्ट 2πrh+2πr2
=2πr(r+h)=S(दिया है )
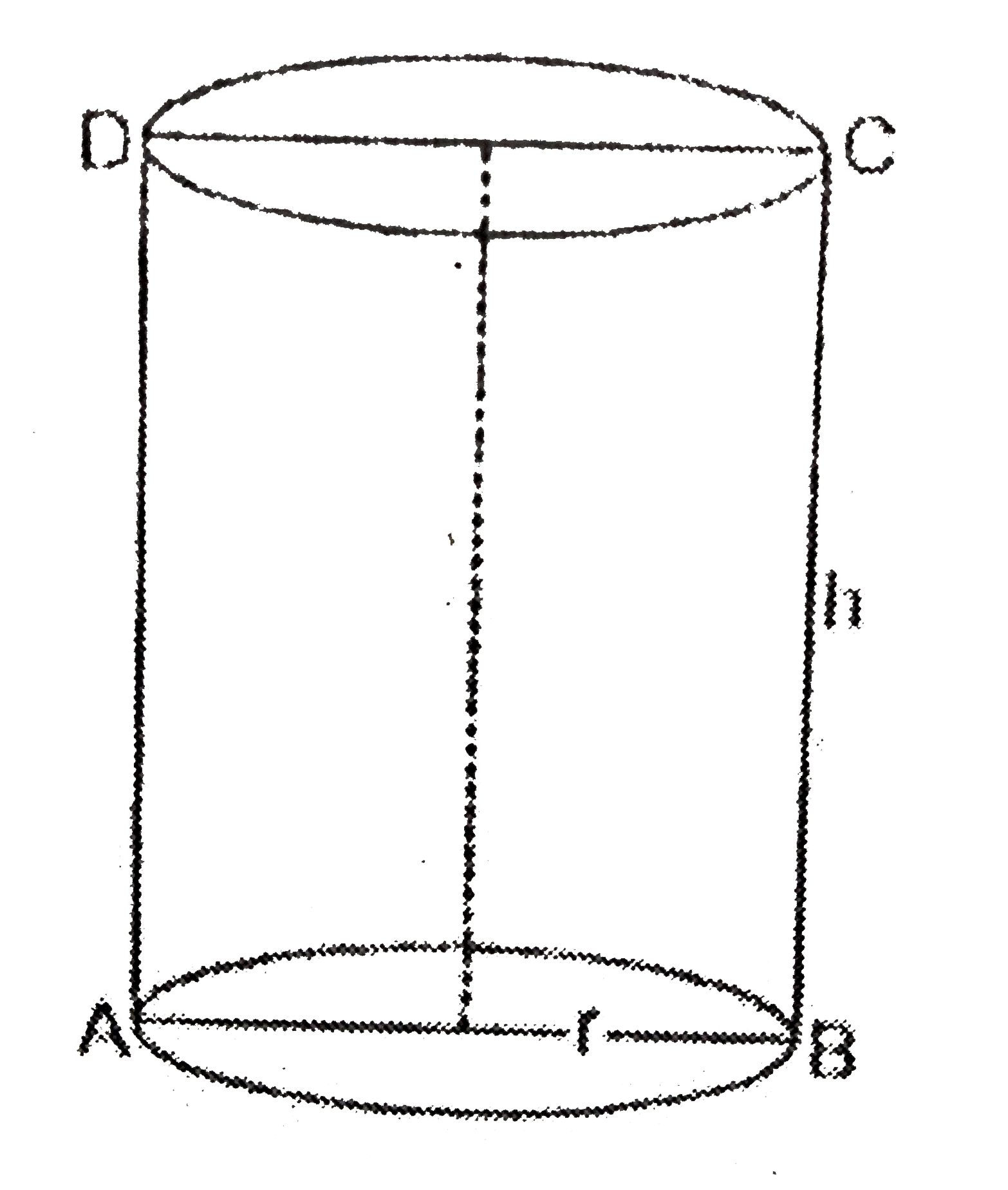
यदि आयतन V है तो V=πr2h
πr2(S2πr−r)=rS2−πr3
यहाँ V चर राशि r का फलन है (S स्थिरांक है)
∴ dVdr=S21−3πr2
तथा d2Vdr=0−6πr=−6πr
V का मान अधिकतम होगा यदि
dVdr=0⇔S2−3πr2=0
⇔ S=6πr2⇔r=√S6π
पुनः जब r=√S6πतो
d2Vdr2=−6π(√S6π)=−√6πS
जो ऋणात्मक है अतः जब r=√S6π तो V अधिकतम है।
पुनः जब r=√S6π तो, h=(S2πr−r)
⇒ h=⎡⎢
⎢⎣S2π√S6π−√S6π⎤⎥
⎥⎦=2√6√Sπ ltbr gt बेलन ऊंचाई की आधार का व्यास=h2r=2√6√Sπ2√S6π=1
अथवा h=2r
जब बेलन की ऊंचाई उसके आधार के व्यास के बराबर है तो उसका आयतन अधिकतम होगा।
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solution10 सेमी. व्यास वाले अर्धगोले का सम्पूर्ण पृष्ट को क्षेत्रफल ज्ञात कीजिए|
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View Solutionजीवन मूल्यों के आधार पर इफ्फन और टोपी शुक्ला के संबंधों की समीक्षा कीजिए।
View Solutionबढ़ती आबादी के पर्यावरण पर पड़ने वाले दुष्प्रभावों की चर्चा करते हुए स्पष्ट कीजिए कि,"नेचर की सहनशक्ति की भी एक सीमा होती है।"
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View SolutionThe radius of a sphere is equal to the base radius and height of a right circular cylinder. What is the ratio between the surface area of the sphere and curved surface area of the cylinder ?
किसी गोले की त्रिज्या, एक लंबवत बेलन (सिलिंडर) के आधार की त्रिज्या तथा ऊंचाई के बराबर है | गोले की पृष्ठभूमि क्षेत्रफल (सरफेस एरिया) तथा बेलन (सिलिंडर) के वक्र पृष्ठ के क्षेत्रफल का अनुपात कितना है ?
View Solution'चाहने वाले की इच्छा सर्वोपरि होती है' के लिए उपयुक्त लोकोक्ति है
View SolutionTi में 'm' के +1 और-1 मान वाले इलेक्ट्रॉनों की अधिकतम संख्या ज्ञात कीजिए।
View Solutionसमान विभवांतर के माध्यम से त्वरित हुए alpha कण और प्रोटॉन के लिए तरंग दैर्ध्य के अनुपात की गणना कीजिए।
View Solutionजब AX और BX2 के जलीय विलयन के माध्यम से विद्युत् के कूलॉम की बराबर संख्या प्रवाहित की जाती है और यदि A और B के निक्षेपित मोलों की संख्या क्रमशः Y और Z है तब-
View Solution
