एल्युमिनियम की 3 मीx 8 मी की आयातकार चादर के प्रत्येक कोने से समान वर्ग काटने पर बने एलुमिनियम के फलकों को मोड़कर ढक्कन रहित एक संदूक बनाना है। इस प्रकार बने संदूक का अधिकतम आयतन ज्ञात कीजिए।
माना आयताकार चादर के चारो कोनों में प्रत्येक की भुजा x सेमि है, जो की वर्गाकार है। माना जब संदूक का आयतन V हो, तब
ltbRgt
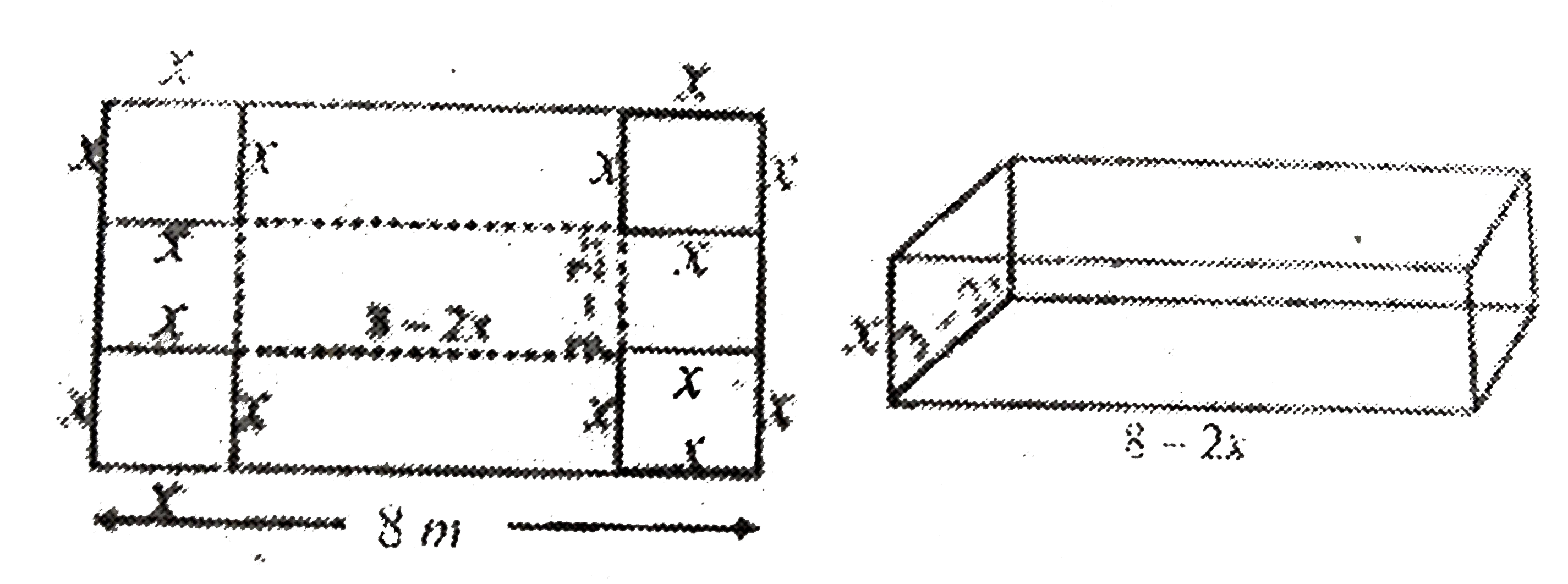
और
चूँकि हो, तब
परन्तु x =3 संभव नहीं है।
अतः
स्पष्टतः
अतः उच्चतम का बिंदु है।
घन मीटर।
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(A)
23 Videos
- अवकलन के अनुप्रयोग BOOK - MANOHAR RAYCHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6(B)
23 Videos
- अवकल समीकरण BOOK - MANOHAR RAYCHAPTER - अवकल समीकरण EXERCISE - प्रश्नावली 9(F)
25 Videos
- आव्यूह BOOK - MANOHAR RAYCHAPTER - आव्यूह EXERCISE - प्रश्नावली 3 (E)
34 Videos
Similar Questions
किसी क्षण t पर एक कण की स्थिति x=4t2−15t+20मीटर से व्यक्त की गयी है।इससे शून्य समय पर कण की स्थति,वेग और त्वरण ज्ञात कीजिए।
View Solutionदिखाइए की निम्नलिखित फलन R पर वर्धमान है।:
(i)f(x)=3x+1
(ii)f(x)=x3−6x2+12x−16
(iii)f(x)=x3−3x2+4x
(iv)f(x)=x+cosx
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
View Solutionबिंदुओं (−3,−1),(−1,3) और (6,2) से बने त्रिभुज के परिकेन्द्र के निर्देशांक ज्ञात कीजिए ।
View Solutionएक दीर्घवृत्त एक धागे से निर्मित किया जाता है, जिसके सिरों को दो पिनों द्वारा स्थिर बिंदुओं S और S' से बाँध दिया है। अब एक पेन्सिल की नोंक से धागे को तानकर उसे कागज पर इस प्रकार चलाया की धागा तना रहे। यदि इस प्रकार बने दीर्घवृत्त के अक्ष क्रमशः 6 सेमी तथा 4 सेमी हों, तो धागे की लम्बाई और पिनों के बीच की दूरी ज्ञात कीजिए।
View Solutionएक घनाकार संदूक के आयतन कि गणना में प्रतिशत त्रुटि ज्ञात कीजिये, जबकि घन कि कोर कि लम्बाई में त्रुटि 5 प्रतिशत होती है।
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 36∘ का कोण बनाती है| बहुभुज की भुजाओं की संख्या ज्ञात कीजिए |
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक समबहुभुज के प्रत्येक बहिष्कोण की माप ज्ञात कीजिए जिसकी
12 भुजाएँ हैं।
View Solution
