Linear simple harmonic motion.
A particle is said to perform linear simple harmonic motion (SHM) if it oscillated about a point of stable equilibrium , subject to a force always directed towards that point and whose magnitude is proportional to the displacement of the particle from the point .
Topper's Solved these Questions
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - ELASTICITY
19 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - SURFACE TENSION
5 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - ROTATIONAL MOTION
3 Videos
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Assignments
9 Videos
Similar Questions
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View SolutionState of differential equation equation of linear simple harmonic motion. Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A body cools from 80∘C to 70∘C in 5 minutes and to 62∘C in the next 5 minutes. Calculate the temperature of the surroundings.
View Solution
Knowledge Check
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
A B
B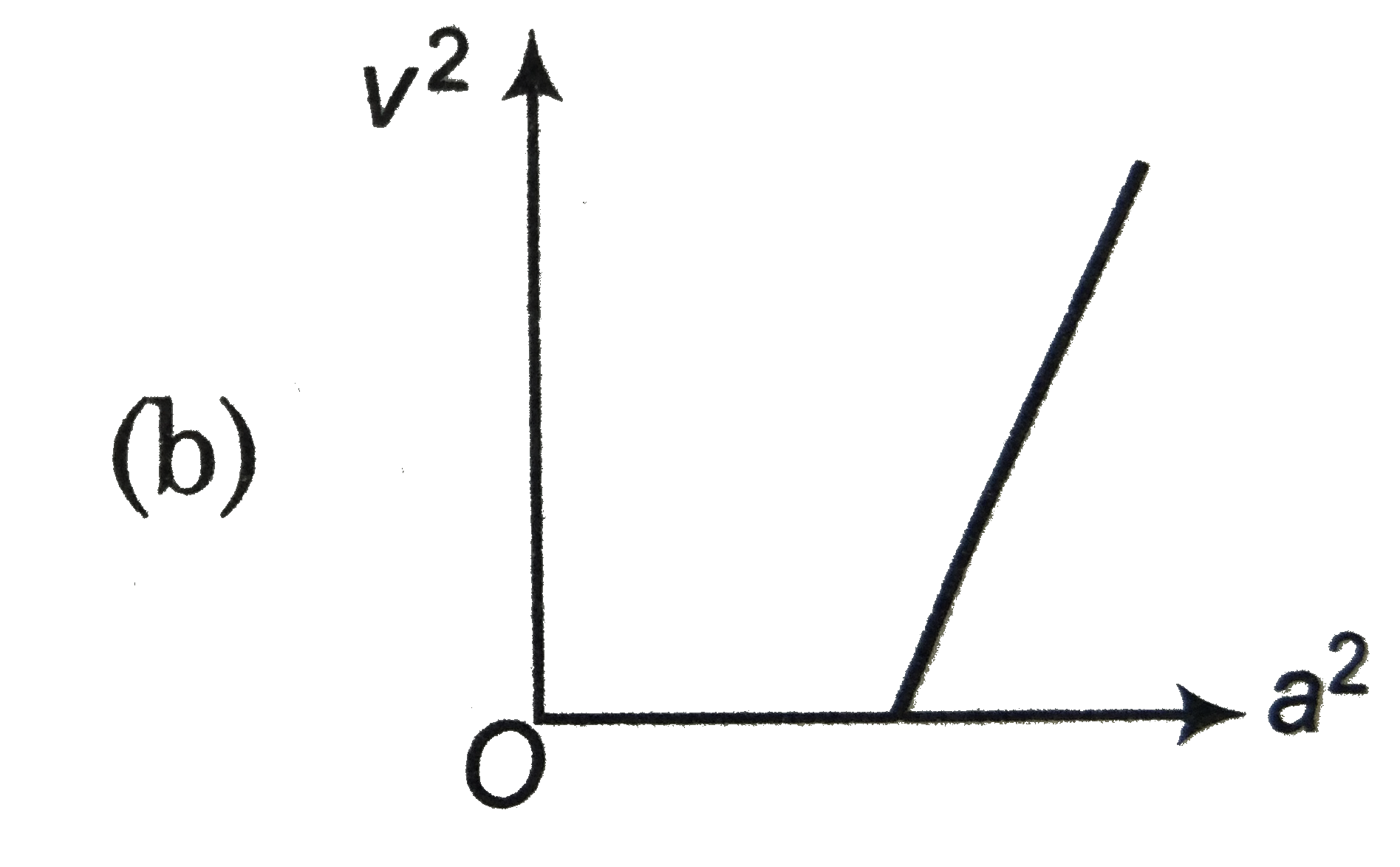 C
C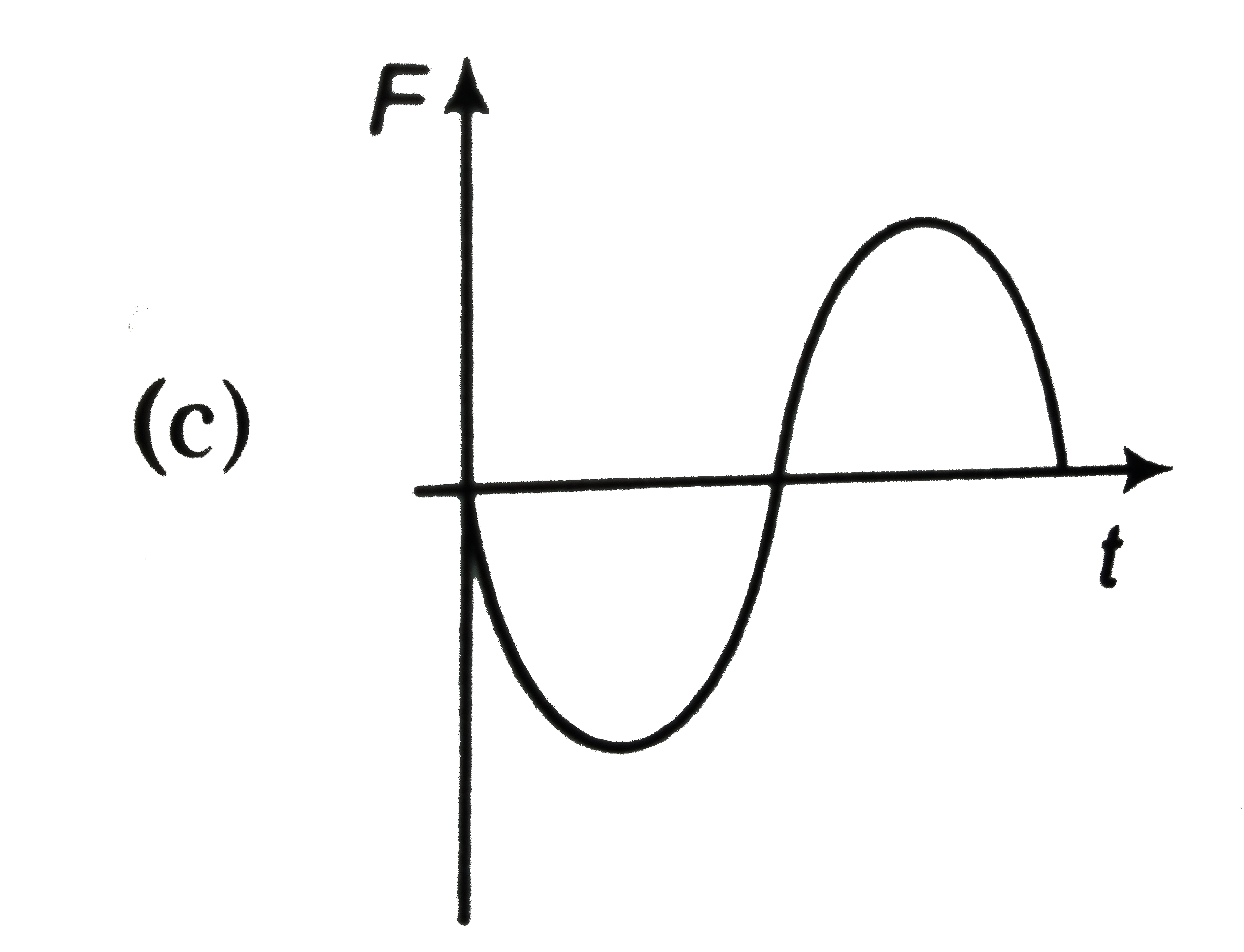 D
D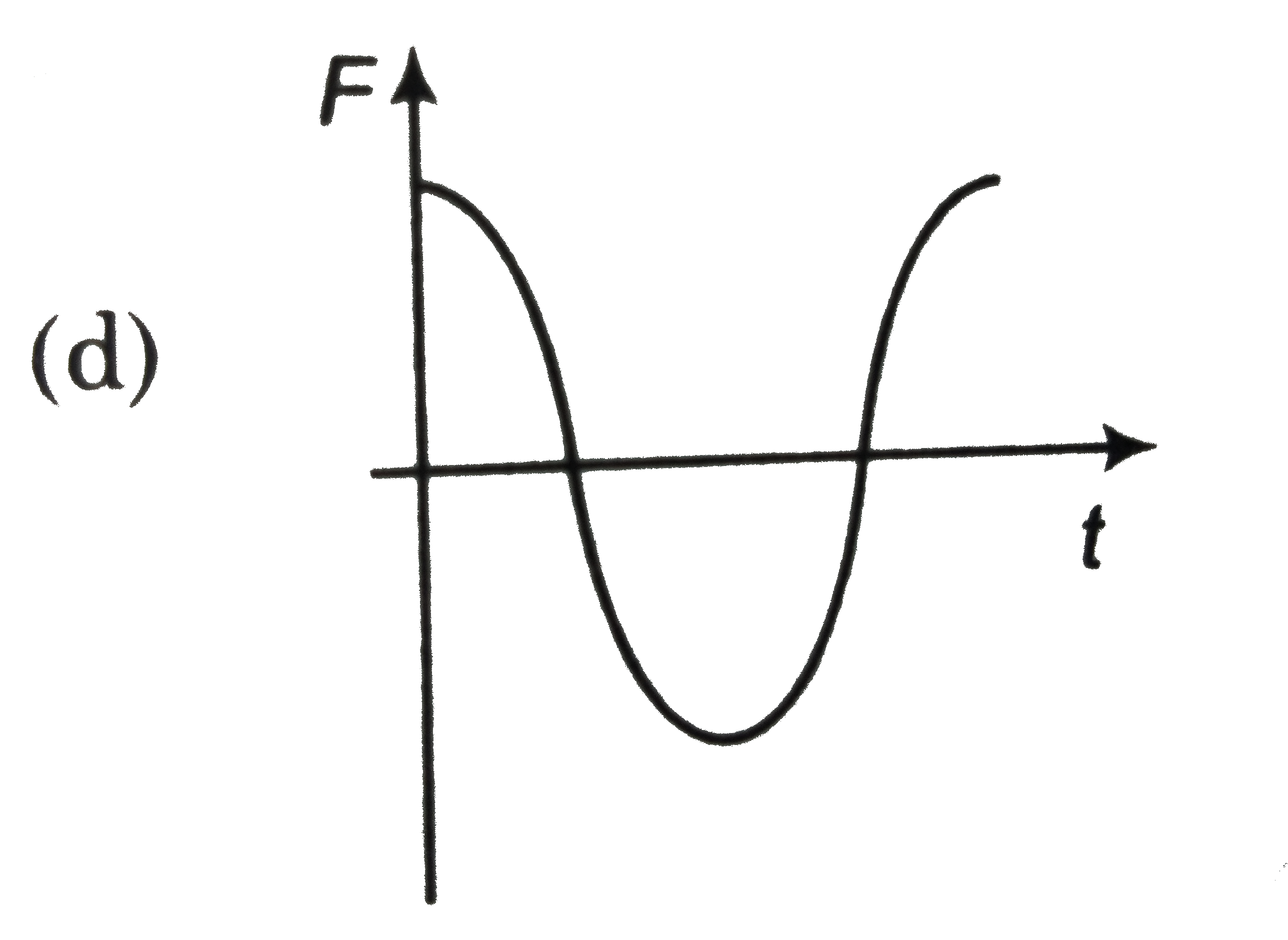
A body is executing a linear simple harmonic motion. At t=0, it is at one of the extreme position and travels 3cm in the first second and 4cm in the next second moving towards the other extreme position .
The amplitude of this S.H.M isA17/18cmB16/17cmC19/18cmD18/5cmA particle executes linear simple harmonic motion with an amplitude of 3cm. When the particle is at 2cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
A√5πB√52πC4π√4D2π√3
A particle executes linear simple harmonic motion with an amplitude of 3cm. When the particle is at 2cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
View SolutionA particle executes linear simple harmonic motion with an amplitude of 2 cm . When the particle is at 1 cm from the mean position the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
View SolutionA particle executies linear simple harmonic motion with an amplitude 3cm .When the particle is at 2cm from the mean position , the magnitude of its velocity is equal to that of acceleration .The its time period in seconds is
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
View Solution
