Moment of inertial .
The moment of inertia of a body about a given axis of rotation is defined as the sum of the products of the masses of the particles of the body and the squares of their respective distances from the axis of rotation.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - OSCILLATION8videos
DEFINITIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - ELASTICITY19videos
DEFINITIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - GRAVITION6videos
DEFINITIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Assignments9videos
DERIVATIONS-I
Similar Questions
A disc with moment of inertial I is rotating with some angular speed. Second disc is initially at rest. Now second disc with moment of inertia 3I is placed on first disc and starts rotating. Find loss of kinetic energy in fraction
View SolutionA solid sphere of mass M and radius R having moment of inertial I about its diameter is recast into a solid disc of radius r and thickness t .The moment of inertia of the disc about an axis passing the edge and perpendicular to the plane remains "I" .Then r=x√15R Find x=?
View Solution
Knowledge Check
- Question 1 - Select One
A bar magnet of magnetic moment M and moment of inertial I is in the direction of magnetic meridian. If the magnet is displaced by a very small angle (θ), the angular acceleration is (Magnetic induction of earth's horizontal field =BH)
AMBHθIBIBHθMCMθIBHDIθMBH - Question 2 - Select One
A disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
AI1ω1I2BI2ω1I2+I2CI1ω2I1+I2D(I1+I2)I2ω1 - Question 3 - Select One
A Moment of inertial of uniform disc and solid cylinder of equal mass and equal radius about an axis passing through centre and perpendicluar to plane will to same.
Moment of inertia depends upon distribution of mass from the axis of rotation i.e., perpendicular distance from the axis.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
The pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
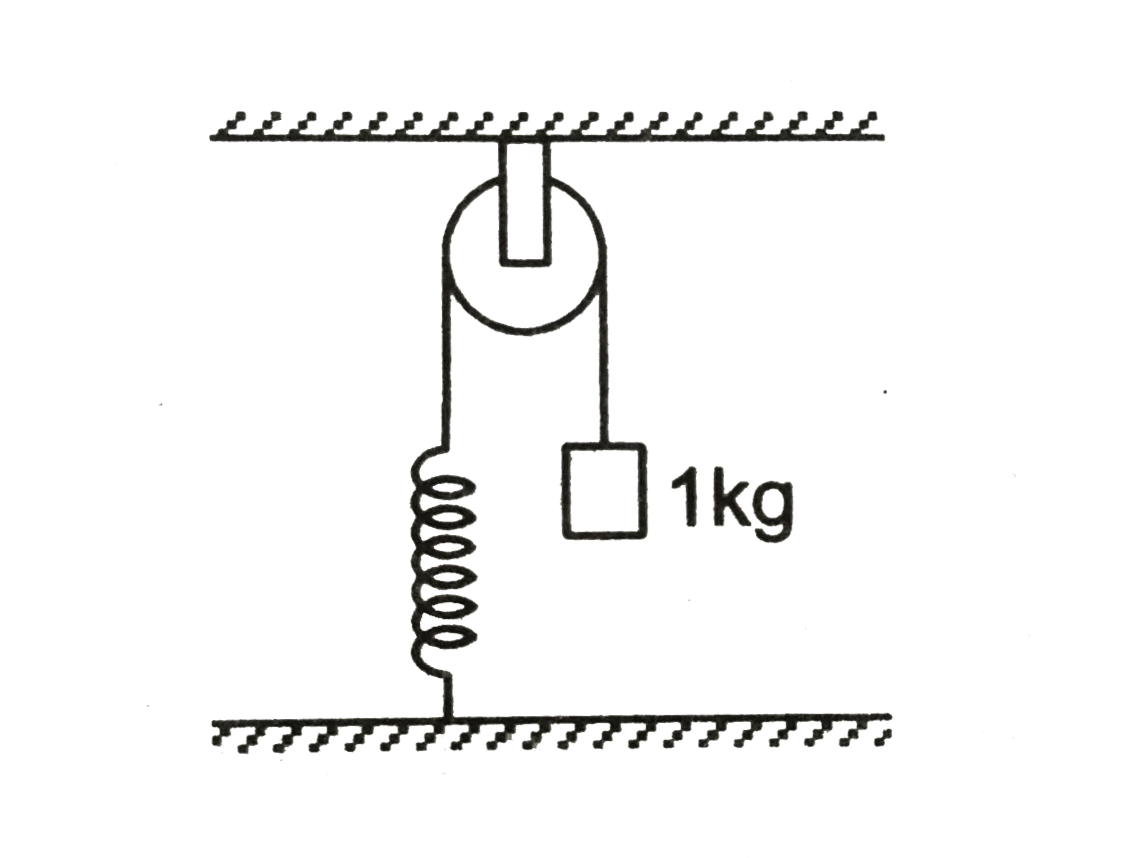 View Solution
View Solution
A thin massless thread is wound on a reel of mass 3 kg and moment of inertial 0.6 kg−m3 the hub radius is R=10cm and peripheral radius is 2R=20 cm the reel is placed on a rough table and the friction is enough to prevent slipping. find the acceleration of the centre of reel and of hanging mass of 1 kg.View SolutionIf I is the moment of inertial of a disc about an axis passing through its centre then find the change in moment of inertial due to small change in its moment of inertia due to small change in its temperature Δt. α is the coefficient of linear expansion of disc.
View SolutionFor a circular cardboard of uniform thickness and mass M, a square disc of the maximum possible are is cut. If the moment of inertia of the square with the moment of inertial of the square with the axis of rotation at the centre and perpendicular to the plane of the disc is Ma26, the radius of the circular cardboard is
View SolutionA rigid body of moment of inertial I is projected with velocity V making an angle of 45∘ with horizontal. The magnitude of angular momentum of the projectile about the point of projection when the body is its maximum height is given by IV32√2gR2 where R is the radius of the rigid body. the ridid body is
View Solution

