A particle of mass m and positive charge q, moving with a uniform velocity v, enters a magnetic field B as shown in Find The radius of the circular are it describes in the magnetic field. (b) find the angle subtended by the arc at the centre. (c ) How long does the particle stay inside the magnetic field? (d) Solve the three parts of the above problem if the charge q on the particle is negative.

(a) Radius of circular are , r = mu/ qB <br>(b)sinceAistan≥nt→areABC,Ang≤describedbythepartic≤,<br> /_MAD = 90^@ <br>Now /_NAC = 90^@ <br>OAC = OCA = q ,<br>[bygaometricalpr∈cipal]<br>ThenAOC=180−(sinθ+thita)
=π−2sinθ
(c ) Distance covered i=rsinθ=r(π−2sinθ)
l=mqB(π−2sinθb)
(d) If the charge 'q' of the particule is negtive , then
(1) Redius of circular are =μqB
(2) In such a case the center of the are will lie within the magnatic field , bence the angle sulitended by the maasure are
=π+2sinθ
(3) Similary the time teken by the
particle to cover the path =mqB(π+sinθ) .
Topper's Solved these Questions
Similar Questions
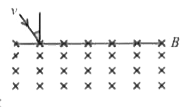
A particle of mass m and positive charge q,moving with a uniform velocity v enters a magnetic field B as shown in figure.(a) Find the radius of the circular arc it describes in the magnetic field. (b)Find the angle subtended by the arc at the centre. (c) How long does the particle stay inside the magnetic field? (d)Solve the three parts of the above problem if the charge q on the particle is negative.
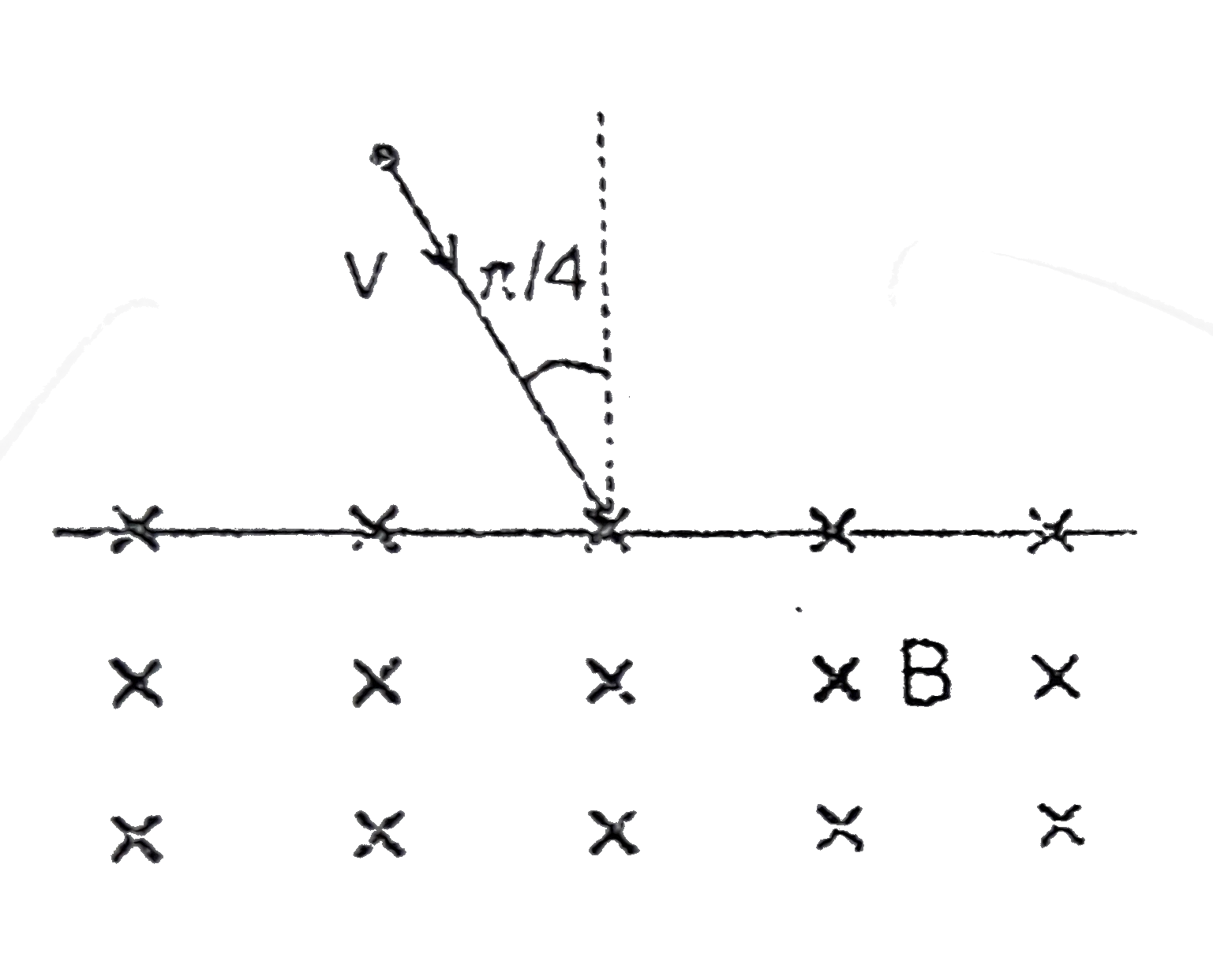
View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View Solution
Knowledge Check
A charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
 ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
ARπθvBR(π−2θ)vCR(π+2θv)D2RθvA particle of mass m and charge q enters a magnetic field B perpendicularly with a velocity v, The radius of the circular path described by it will be
ABq/mvBmq/BvCmB/qvDmv/BqA particle of mass m, charge e and velocity v moving in a magnetic field B perpendicular to the motion of particle. The radius of its path is:
ABemvBevBmCBvemDmvBe
A particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionTwo particles having identical masses and charges 2Q and Q are moving with velocities v and 2v resp. In uniform magnetic field B. Find ratio of radius of circle described by them
View SolutionA particle carrying a charge moves perpendicular to a uniform magnetic field of induction B with a momentum p then the radius of the circular path is
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View SolutionA charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
View Solution
