A rectangular coil of 100 turns has length 5 cm and width 4 cm. it is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B, if the torque acting on the coil is 0.2Nm−1.
To solve the problem step by step, we will use the formula for torque acting on a rectangular coil in a magnetic field. The torque (τ) on a coil is given by the formula:
τ=n⋅B⋅I⋅A⋅sin(θ)
Where:
- τ = Torque (in Nm)
- n = Number of turns in the coil
- B = Magnetic field strength (in T)
- I = Current (in A)
- A = Area of the coil (in m²)
- θ = Angle between the magnetic field and the normal to the coil's plane
Since the coil is placed with its plane parallel to the magnetic field, the angle θ is 90 degrees, and sin(90∘)=1. Therefore, the formula simplifies to:
τ=n⋅B⋅I⋅A
Step 1: Calculate the area of the coil
The area A of the rectangular coil can be calculated using the formula:
A=length×width
Given:
- Length = 5 cm = 0.05 m
- Width = 4 cm = 0.04 m
Calculating the area:
A=0.05m×0.04m=0.002m2
Step 2: Substitute the known values into the torque formula
Now we can substitute the known values into the torque equation:
Given:
- n=100 turns
- I=2A
- τ=0.2Nm
- A=0.002m2
The equation becomes:
0.2=100⋅B⋅2⋅0.002
Step 3: Simplify the equation
Now simplify the right-hand side:
0.2=100⋅B⋅0.004
Calculating 100⋅0.004:
100⋅0.004=0.4
So the equation now is:
0.2=0.4⋅B
Step 4: Solve for B
Now, solve for B:
B=0.20.4=0.5T
Final Answer
The magnitude of the magnetic field B is 0.5T.
---
- τ = Torque (in Nm)
- n = Number of turns in the coil
- B = Magnetic field strength (in T)
- I = Current (in A)
- A = Area of the coil (in m²)
- θ = Angle between the magnetic field and the normal to the coil's plane
- Length = 5 cm = 0.05 m
- Width = 4 cm = 0.04 m
- n=100 turns
- I=2A
- τ=0.2Nm
- A=0.002m2
Topper's Solved these Questions
Similar Questions
A square coil of 600 turns, each side 20cm, is placed with its plane inclined at 30∘ to a uniform magnetic field of 4.5×10−4Wbm−2, Find the flux through the coil.
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View Solution
Knowledge Check
A rectangular coil has 100 turns has length 5 cm and breadth 2 cm. It is suspended in radial magnetic field of induction 0.1 Wb/m2. If a current of 100 μA is passed through the coil, then the torque acting on the coil is
A10−6 N mB10−7 N mC10−5 N mD10−8 N mA circular coil of 1 turn and area 0.01m2 carries a current of 10A. It is placed in a uniform magnetic field of induction 0.1 tesla such that the plane of the circle is perpendicular to the direction of the field, the torque acting on the coil is
A0.1NmB0.001NmC0.01NmDZeroA circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
A 100 turns coil shown in figure carries a current of 2 amp in a magnetic field B=0.2Wb/m2. The torque acting on the coil is
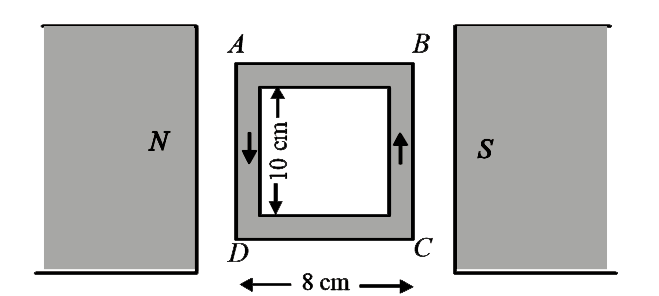
View SolutionIf plane of coil and uniform magnetic field B(4T0 is same then torque on the current carrying coil is

View SolutionA wire is bent to form a circular coil of radius 5 cm with 20 loops. The coil is placed in a magnetic field of 0.5 T and a current of 1 A flow through it. Calculate the maximum torque exerted by magnetic field.
View SolutionA current of 5A flows through a circular coil of 200 turns, each of radius 20 cm. It is placed in a uniform magnetic induction of 5×10−2 Wb/m2, such that the plane of the coil is parallel to the field. What is the torque acting on the coil?
View SolutionA rectangular coil of area→Aand number of turns n is placed in a uniform magnetic field vecB. If the coil carries a current I, then the torque acting on the coil is given by
View Solution