Consider a non conducting plate of radius a and mass m which has a cha

Consider a solid sphere of radius r and mass m which has a charge q distributed uniformly over its volume. The sphere is rotated about a diameter with an angular speed $ω$ . The magnetic moment of the sphere is
A $\frac{1}{3} q ω r^{2}$
B $\frac{1}{5} q ω r^{2}$
C $\frac{1}{7} q ω r^{2}$
D $\frac{1}{9} q ω r^{2}$
A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity $ω$ . The magnetic moment of the arrangement is
A $\frac{Q R^{2} ω}{8}$
B $\frac{Q R^{2} ω}{4}$
C $\frac{Q R^{2} ω}{2}$
DZero
A disc of mass $m$ has a charge $Q$ distributed on its surface. It is rotating about an $X X'$ with a angular velocity $ω$ . The force acting on the disc is

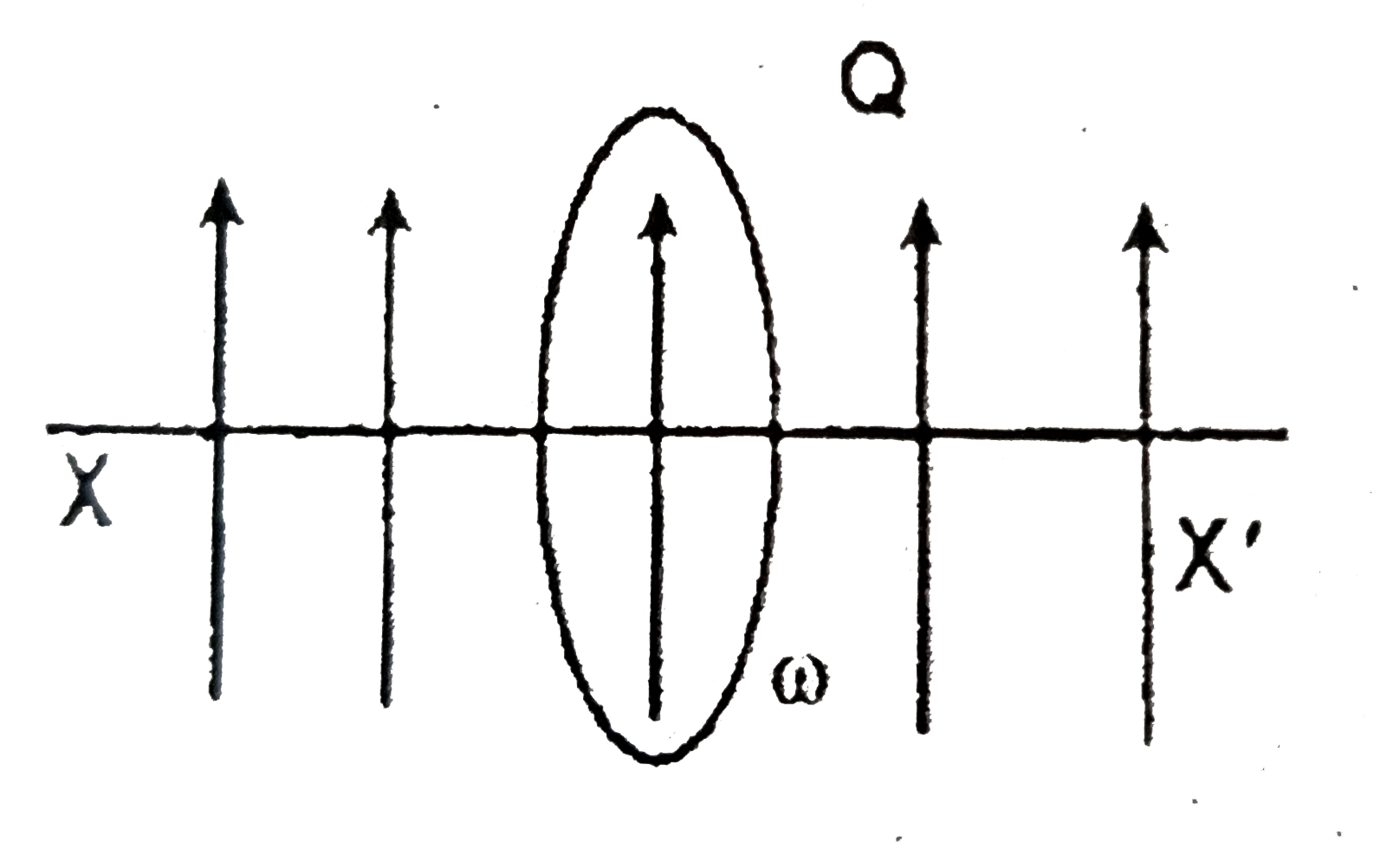Azero
B $ω R B / π$
C $2 Q ω B R$
Dnone of these

Since $I = \frac{q v}{2 π r}$
So , magnetic
$μ = i a = \frac{q v}{2 π r} π r^{2}$
$\Rightarrow μ = \frac{q μ r}{2 m} = \frac{q}{2 m} l$