A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultantant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
The magnetic field will be maximum at point P whare net magnetic field =B+μ0i2πr
.(b)mag≠ticfieldB=0whenrlt(mu_0i)/(2piB)<br>. But when r>μ0i2πB
.Netmag≠ticfield=B−μ0i2pr.
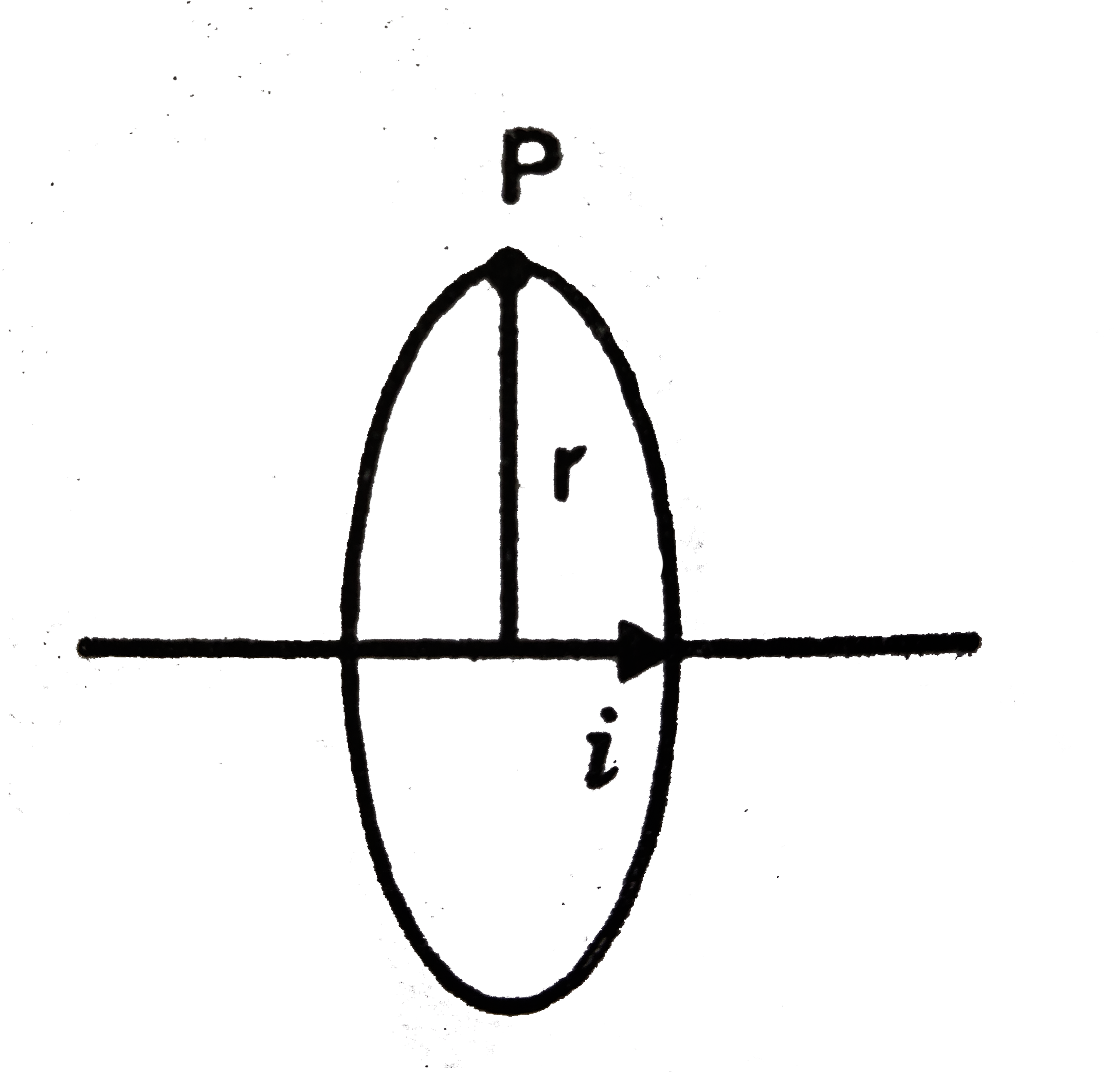
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
Knowledge Check
A semicircular wire of radius r, carrying a current I, is placed in a magnetic field of magnitude B. The force acting on it
Acan never be zeroBcan have maximum magnitude 2BIrCcan have the maximum magnitude BIπrDcan have the maximum magnitude BIr
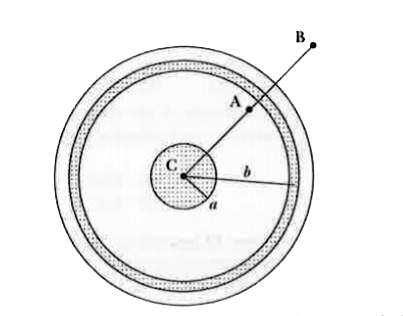 What is the magnitude and direction of the magnetic field at point B ?A3.3×10−5 T, clockwiseB6.8×10−5 T, counterclockwiseC3.3×10−5 T, counterclockwiseD2.7×10−4 T, clockwise
What is the magnitude and direction of the magnetic field at point B ?A3.3×10−5 T, clockwiseB6.8×10−5 T, counterclockwiseC3.3×10−5 T, counterclockwiseD2.7×10−4 T, clockwiseA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1
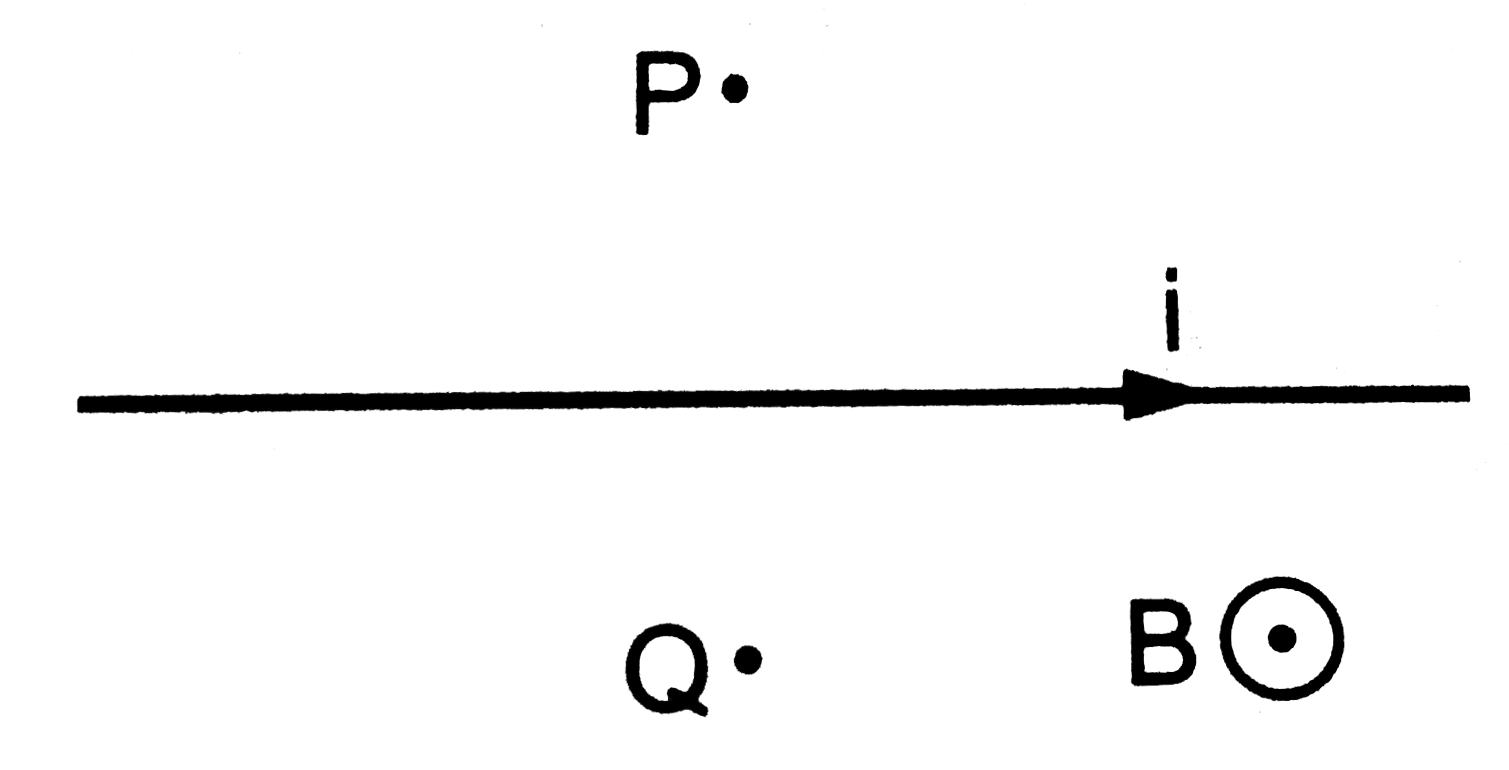
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B= (1.0×10−5) T pointing vertically upward. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionA long straight wire of circular cross section is Made of non-Magnetic Material.The wire of radius (a).The wire carries a current (I) which is uniformly distributed over its cross-section.The energy stored per unit length in Magnetic field contained within the wire.
View Solution
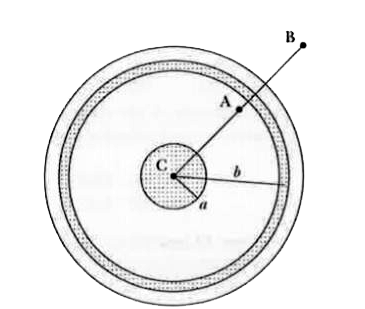
What is the magnitude and direction of the magnetic field at point A ?
View SolutionA very long straight wire of radius 'r carries current 'I'. Intensity of magnetic field 'B' at a point, lying at a perpendicular distance 'a' from the axis is ∝ ___________
View Solution
