Consider the situation of the previous problem. Find the average electric field energy stored in the capacitor and the average magnetic field energy stored in the coil.
Video Solution
Text Solution
Given R=300Ω, C=20μF
=20×10−6F, L=1H, Z=500(from 14) ,E0=50V, i0=E0Z=50500=0.1A
Electrical energy stored in capacitor
=12CV2
=12×20×10−5×50×50
=25×10−3J=25mJ.
Magnetic field energy stored in the coil
=12Li20
=12×1×(0.1)2
=12×1×10−2=5×10−3J
=5mJ
|
Topper's Solved these Questions
Similar Questions
(a) In a series L-C-R circuit with an AC source, R =300Ω, C = 20μF,L=1.0H,V0=50√2Vandf=50πHz. Find (i) the rms current in the circuit and (ii) the rms voltage across each element.
(b) Consider the situatiuon of the previous part. find the average electric field energy stored in the capacitor and the average magnetic field energy stored iun the coil .
View SolutionWhere is energy stored in a capacitor?
View Solution
Knowledge Check
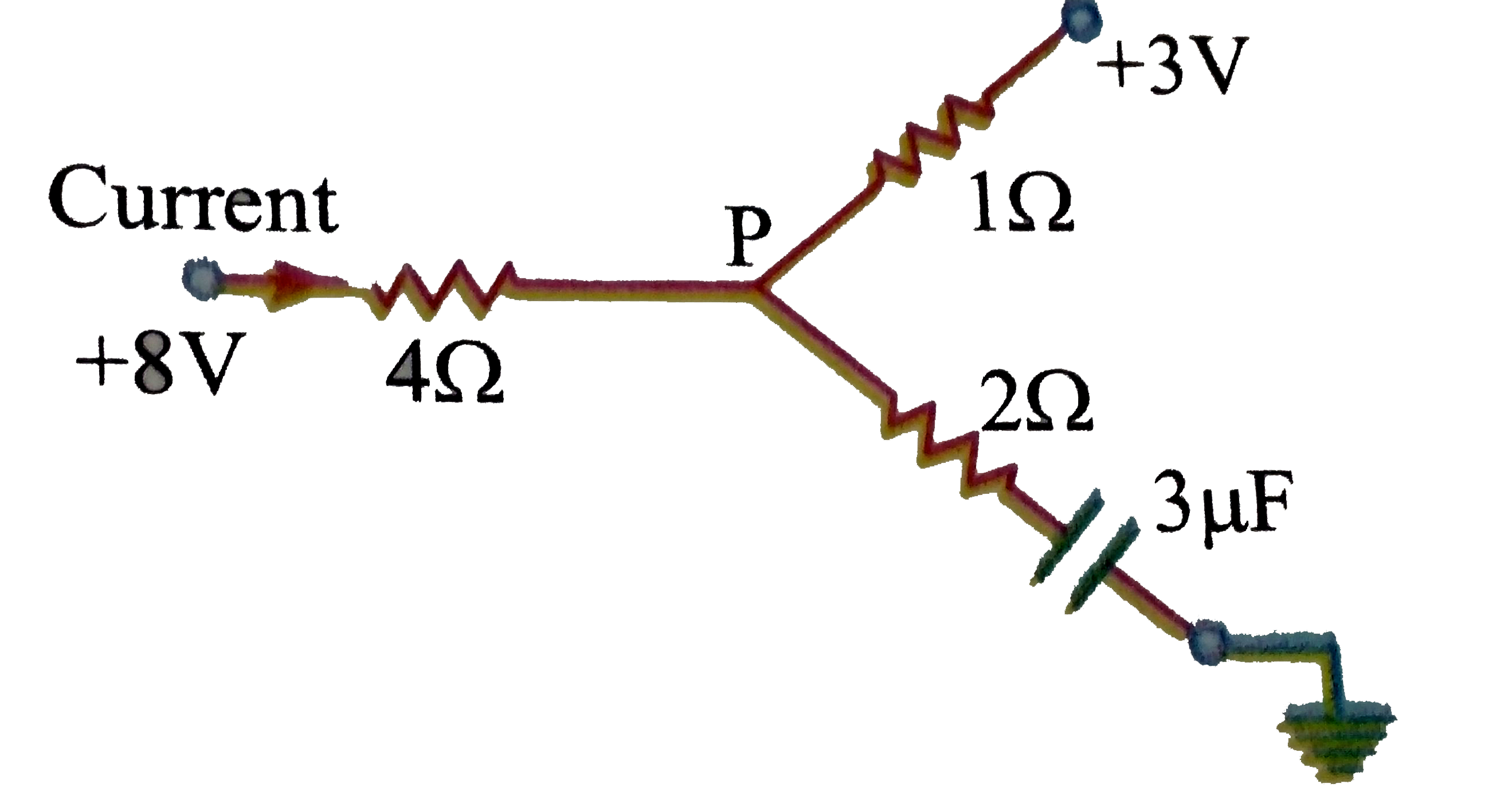
the energy stored in the capacitor isA12μJB24μJC36μJD48μJMagnetic field energy stored in a coil is
ALi2B12LiCLiD12Li2Energy Stored in the capacitor is
Aε0E2×AdB(12)ε0E2×AdCε0E2×AdDε0E×Ad
The electric energy stored in a cube

View SolutionThe energy stored in the capacitor in the steady state is
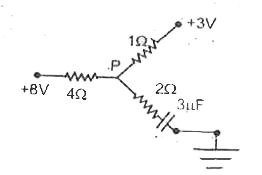
View SolutionThe energy stored in the capacitor in the steady state is
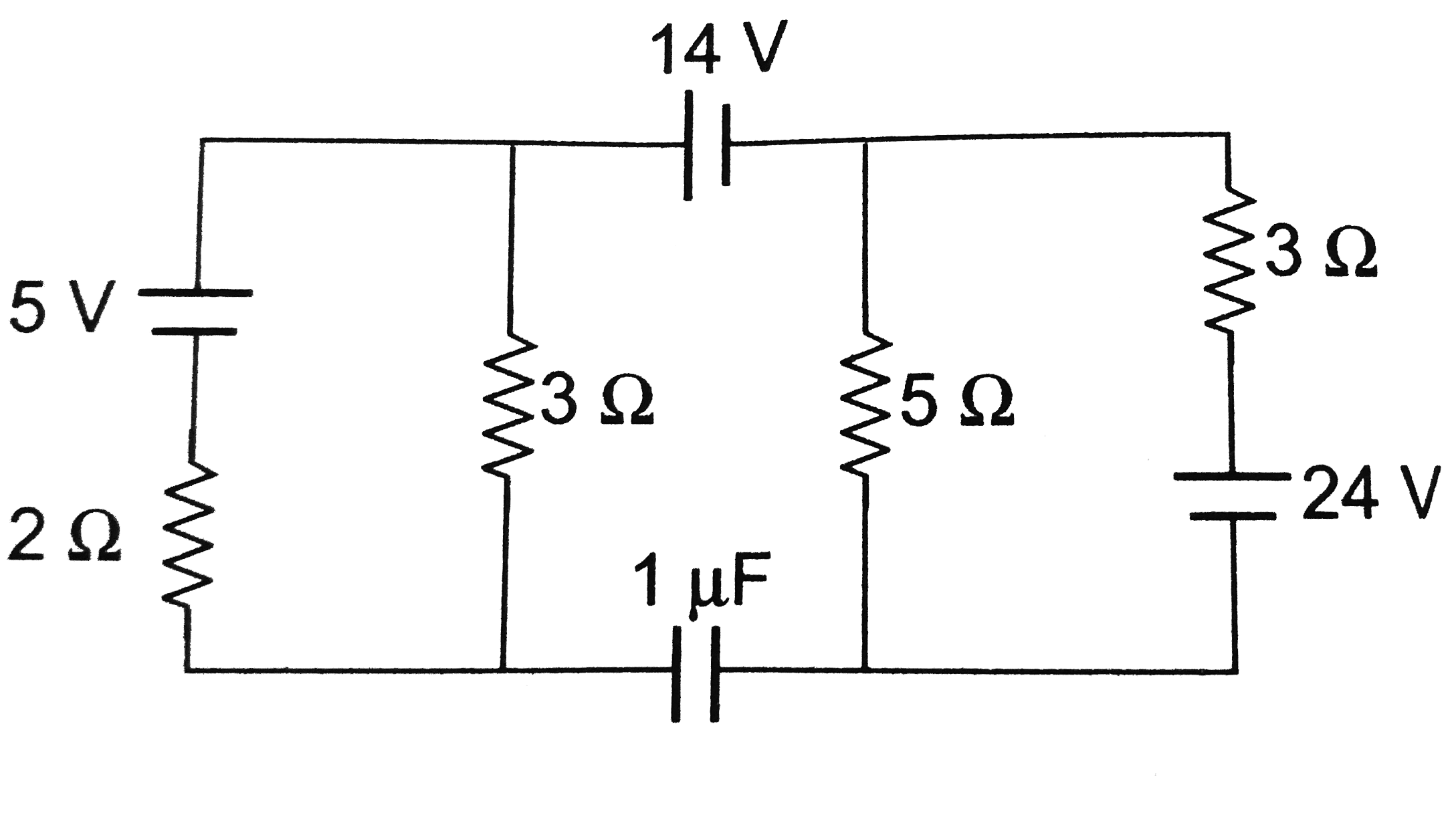
View SolutionIn the figure magnetic energy stored in the coil is

View SolutionIn steady state, find energy stored in the capacitor -

View Solution
