Theorem 7.6 : If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater)
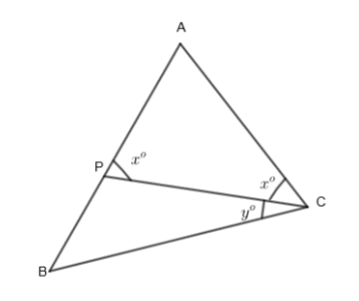
Let us assume a triangle ABC such that the sides are as AB>AC.
Now, take a point P on line AB such that AP=AC. Join the two points C and P to set CP. Let us assume angle APC is x and angle BCP is y.
.
We know that AP=AC.
If two sides are equal in a triangle, then the angles opposite to the sides are equal. Applying this condition to the triangle APC, we get the angle APC and angle ACP, all equal. As angle APC is x,
we get the angle ACP also x.
Mathematically, we write these steps as follows:
∠ACP=∠APC
∠ACP=x
On line AB, we can say that it is a straight line which is equal to 180
So, we get,
∠APC+∠CPB=180
By substituting the value of angle APC, we get the equation as,
x+∠CPB=180
By subtracting x on both the sides of the equation, we get it as,
∠CPB=18o−x
We know the theorem that sum of all the angles in a triangle is 180.
By applying this to the triangle CPB, we get it as,
∠CBP+∠BPC+∠PCB=180
By substituting the value of BPC from the above equation, we get,
∠CBP+180−x+∠PCB=180
By substituting the value of PCB as per our assumption, we get,
∠CBP+180−x+y=180
By canceling out the common terms, we can write it as,
∠CBP−x+y=0
By adding x and subtracting y on both the sides, we get,
∠CBP=x−y
From the diagram, we can say that,
∠CBP=∠CBA
∠CBA=x−y
From the diagram, we can say that,
∠BCA=∠BCP+∠PCA
By substituting the values, we get it in the form of
∠BCA=x+y
From above equations, we can say the inequality in the form of
∠BCA>∠CBA
Hence, we have proved that the angle opposite to the greater side is larger.
Topper's Solved these Questions
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.7
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.8
Explore 1 Video
- NCERT THEOREMSBook:NCERTChapter:NCERT THEOREMSExercise:THEOREM 7.5
Explore 1 Video
- LINES AND ANGLESBook:NCERTChapter:LINES AND ANGLESExercise:SOLVED EXAMPLES
Explore 8 Videos
- NUMBER SYSTEMSBook:NCERTChapter:NUMBER SYSTEMSExercise:EXERCISE 1.4
Explore 2 Videos
Similar Questions
If two angles of a triangle are equal;then sides opposite to them are also equal.
View SolutionIf two sides of a triangle are unequal; the longer side has greater angle opposite to it.
View SolutionIn a triangle the angle opposite the largest side is the largest.
View SolutionIf two sides of a triangle are inequal , then the larger side has _______ angle opposite to it .
View SolutionIn a triangle the greater angle has the longer side opposite to it.
View SolutionTest the validity of the following argument :
S1 : If two sides of a triangles are equal, then the opposite angles are equal.
S2 : Two sides of a triangle are not equal
S : Two opposite angles are not equal.
View SolutionFill in the blanks to make the following statements true: In a right triangle the hypotenuse is the ...... side. The sum of three altitudes of a triangle is ......... than its perimeter. The sum of any two sides of a triangle is ......... than the third side. If two angles of a triangle are unequal, then the smaller angle has the ........... side opposite to it. Difference of any two sides of a triangle is ......... than the third side. If two sides of a triangle are unequal, then the larger side has ..... angle opposite to it.
View SolutionWhich of the following statements are true (T) and which are false (F)? Sum of the three sides of a triangle is less than the sum of its three altitudes. Sum of any two sides of a triangle is greater than twice the median drawn to the third side. Sum of any two sides of a triangle is greater than the third side. Difference of any two sides of a triangle is equal to the third side. If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it. Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionIf two angles of a triangle are unequal , then the smaller angle has the ________ side opposite to it .
View SolutionTheorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
View Solution