Theorem 7.7 : In any triangle, the side opposite to the larger (greater) angle is longer
Let us assume AC>AB
then ∠B>∠C
Which contradicts our assumption.
Hence, AB>AC.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.81videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 8.11videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.61videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.42videos
NUMBER SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
In any triangl, the side opposite to the greater angle is longer.
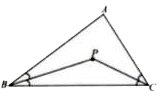
In a ΔABC, if ∠A=45∘,∠B=70∘. The largertst side of a triangle isABCBABCACDNone of these - Question 2 - Select One
In any triangl, the side opposite to the greater angle is longer.
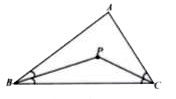
In ΔABC if ∠C>∠B thenABC>ACBAB>ACCAB<ACDBC<AC - Question 3 - Select One
The side opposite to an obtuse angle of a triangle is :
AsmallestBgreatestChalf of the perimeterDnone of these
Theorem 7.6 : If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater)
View SolutionProve the following statement. "The bisector of an angle of a triangle divides the sides opposite to the angle in the ratio of the remaining sides"
View SolutionTheorem 7.3 : The sides opposite to equal angles of a triangle are equal.
View SolutionTheorem 6.9 : In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
View SolutionFind the odd statement out in relation to a triangle .
A . The logest side is opposite to the greatest angle.
B. The exterior angle of triangle is the sum of interior opposite angle.
C. The sum of any 2 sides is greater than the 3rd side.
D. The sequare of one side = the sum of the squares of other tow sides .View Solution

